物理学的公式很多,而且某个物理量的公式往往不止一个,如何记住这些公式并能恰当地运用是学生感到非常头痛的问题。如果对物理公式的特征、规律进行全面的整合,记住更多的公式也不会很难,而且在运用中也不会乱套公式。
中学物理公式主要分为三大类,一类是定义式,一类是关系式,一类是决定式。这样分类是从公式的特征来区分的。
一、定义式的种类及特征
物理量的定义方法有六种。
一是比值定义法。用这种方法定义的物理量一般来说是反映物体的某种特性,这些比值的大小是由物体本身的某种属性所决定,与定义式中出现的其他量无关,比值是一个定值。如速度(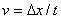 )、功率( )、功率(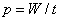 )、电场强度( )、电场强度(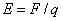 )、电容( )、电容(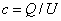 )等。在物理公式中,所有用比值定义的物理量(压强的定义式除外)都与公式中出现的其他物理量之间没有正反比关系。 )等。在物理公式中,所有用比值定义的物理量(压强的定义式除外)都与公式中出现的其他物理量之间没有正反比关系。
二是乘积定义法。对于用这种方法定义的物理量应从它所能产生的效果去认识它的特性,如动能(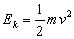 )、动量( )、动量(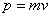 )、功( )、功( )、磁通量( )、磁通量(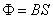 )等,这种定义式反映物理量之间的函数关系。如公式 )等,这种定义式反映物理量之间的函数关系。如公式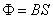 中 中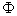 与磁感应强度 与磁感应强度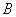 成正比,与处在磁场中垂直于磁场方向的面积 成正比,与处在磁场中垂直于磁场方向的面积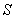 成正比。 成正比。
三是差值定义法。一般用来定义某个物理量的变化量,这种定义式反映物理量之间的一种简单的变化关系。如位移的变化(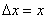 2 2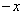 1),磁通量的变化( 1),磁通量的变化(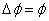 2 2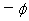 1),电势差( 1),电势差(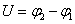 )等。 )等。
四是和值定义法。一般用来定义几个同类物理量的和,这种定义式反映几个同类物理量之间的等效关系。如合力(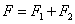 )、合位移( )、合位移(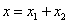 )、总功( )、总功(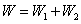 )、总电阻( )、总电阻(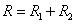 )等。 )等。
在和值定义法和差值定义法中,是矢量的遵循矢量的运算法则,是标量的遵循代数运算。
五是函数定义法。一般用来定义按一定规律变化的物理量,如正弦交流电的电流(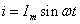 )、简谐振动的位移( )、简谐振动的位移( ),这种定义式反映一种变化规律,即一定的函数关系。 ),这种定义式反映一种变化规律,即一定的函数关系。
六是极限定义法。一般用来定义某一时刻的状态量,如速率(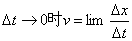 )、瞬时加速度( )、瞬时加速度(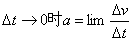 )等,这种定义式反映物理量在某一时刻的状态。 )等,这种定义式反映物理量在某一时刻的状态。
二、平均值公式和瞬时值公式
有的物理公式有平均值公式和瞬时值公式,这样分类是从公式的时间特征来区分的。平均值公式对应某一过程,如平均速度对应质点在某一段位移内速度的平均值;法拉第电磁感应定律公式(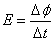 )对应磁通量发生了 )对应磁通量发生了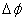 的变化时感应电动势的平均值。这种公式反映某种变化的一种平均效应,与事实发生的某一过程相对应。 的变化时感应电动势的平均值。这种公式反映某种变化的一种平均效应,与事实发生的某一过程相对应。
瞬时值公式对应某一时刻,如瞬时速度是运动物体在某一时刻的速度;电磁感应现象中动生感应电动势公式(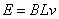 )对应导体的运动速度为 )对应导体的运动速度为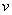 时的感应电动势;交变电流公式( 时的感应电动势;交变电流公式(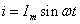 )在每一时刻都是变化的等。这种公式反映某一时刻的一种状态,总是与某一时刻相对应。 )在每一时刻都是变化的等。这种公式反映某一时刻的一种状态,总是与某一时刻相对应。
三、定理和定律公式
定理和定律公式属于关系式,是对事物间所遵循的规律或规则的一种公式表述,是对某种关系的简洁叙述,如动能定理公式(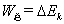 ),动量守恒定律公式( ),动量守恒定律公式(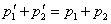 )等,这种公式反映在某一特定的条件下,物理过程所遵循的规律,总是与特定的条件和特定的过程相对应。对于这类公式的理解和掌握,一定要透彻理解定理、定律的内容,特别是其的条件。 )等,这种公式反映在某一特定的条件下,物理过程所遵循的规律,总是与特定的条件和特定的过程相对应。对于这类公式的理解和掌握,一定要透彻理解定理、定律的内容,特别是其的条件。
四、两大特征、一大规律
对中学物理公式进行分类整合以后,还要注意“两大特征、一大规律”:
1、两大特征:
(1)对于定义式,具有普遍意义,是普适公式;对于关系式和决定式,往往是由某种特殊情况得出,所以适用范围较小,只在一定的条件下成立。如电流的三个公式,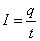 是定义式,适用于所有的电路, 是定义式,适用于所有的电路,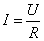 是决定式,只适用于线性元件, 是决定式,只适用于线性元件,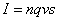 是电流的微观关系式,只适用于金属或电解液;又如电场强度的三个公式: 是电流的微观关系式,只适用于金属或电解液;又如电场强度的三个公式: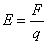 是定义式,适用于所有电场, 是定义式,适用于所有电场,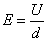 是关系式,只适用于匀强电场, 是关系式,只适用于匀强电场,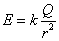 是决定式,只适用于真空中的点电荷的电场。 是决定式,只适用于真空中的点电荷的电场。
(2)凡是用比值定义物理量得到的定义式(比值定义式)都没有正反比关系(压强的定义式除外),用其它方式定义的公式一般有函数关系。注意这里“凡是”的内函:定义式+比值=比值定义式。如加速度的公式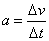 是比值定义式, 是比值定义式,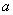 与 与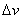 无正比关系,与 无正比关系,与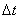 无反比关系, 无反比关系, 是决定式, 是决定式,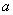 与 与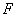 成正比,与 成正比,与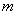 成反比,这两个公式都是比值的形式,但一个没有函数关系,一个有函数关系;又如 成反比,这两个公式都是比值的形式,但一个没有函数关系,一个有函数关系;又如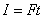 是冲量的定义式,不是用比值的方法定义的, 是冲量的定义式,不是用比值的方法定义的,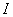 与 与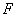 和 和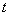 成正比,有函数关系。 成正比,有函数关系。
2、一大规律:
凡是与过程有关的运算就优先使用平均值公式,凡是与时刻有关的运算就优先使用瞬时值公式。如一质点以加速度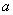 做初速度为 做初速度为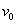 的匀加速度直线运动,运动一段时间 的匀加速度直线运动,运动一段时间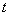 ,求质点在这段时间 ,求质点在这段时间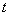 内的平均速度和中间时刻的瞬时速度;一正方形线圈边长为 内的平均速度和中间时刻的瞬时速度;一正方形线圈边长为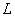 ,在磁感应强度为 ,在磁感应强度为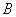 的匀强磁场中以角速度 的匀强磁场中以角速度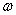 匀速转动,求线圈从中性面开始转过 匀速转动,求线圈从中性面开始转过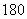 0这一过程的感应电动势和线圈中的最大感应电动势。以上两例中,求前一个量都用平均值公式,求后一个量都用瞬时值公式。 0这一过程的感应电动势和线圈中的最大感应电动势。以上两例中,求前一个量都用平均值公式,求后一个量都用瞬时值公式。
对物理公式的特征、规律以及应用原则有了较全面的归纳整合,对于物理公式的理解、记忆及应用,可以收到事半功倍之效,就不会出现以偏概全、模棱两可、乱套公式的现象。
赵 斌 (湖南省长沙市第六中学 410000)
|

