|
2010届高三物理三轮复习-基础知识查漏
一.质点的运动(一)------直线运动
1)匀变速直线运动
1.平均速度V平=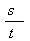 (定义式) (定义式)
2.有用推论 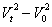 =2as =2as
3.中间时刻速度Vt/2=V平=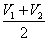
4.末速度Vt=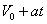 = = 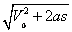
5.中间位置速度VS/2= 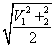
6.位移s=V平t=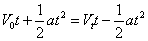
7.加速度a=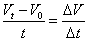 {以Vo为正方向,a与Vo同向(加速)a>0;反向则a<0} {以Vo为正方向,a与Vo同向(加速)a>0;反向则a<0}
8.实验用推论Δs= 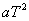 {Δs为连续相邻相等时间T内位移之差} {Δs为连续相邻相等时间T内位移之差}
组差法求纸带加速度a= 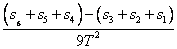
9.匀变速直线运动的比例:
①初速为零的匀加速直线运动,在1s 、2s、3s……ns内的位移之比为:12:22:32……n2;
② 在第1s 内、第 2s内、第3s内……第ns内的位移之比为1:3:5……(2n-1);
③ 在第1米内、第2米内、第3米内……第n米内的时间之比为
1: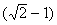 : :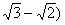 ……( ……(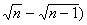
④初速无论是否为零,匀变速直线运动的质点,在连续相邻的相等的时间间隔内的位移之差为一常数:Ds = aT2 (a一匀变速直线运动的加速度 T一每个时间间隔的时间)
10. s--t图、v--t图.图像的物理意义位移随时间的变化关系和速度随时间的变化关系,截距的物理意义s--t图 中与纵轴交点表示位置点,截距表示位移;与横轴交点表示时刻,截距表示时间。v--t图中与纵轴交点表示速度,截距表示速率;与横轴交点表示时刻,截距表示时间。斜率的物理意义 s--t图 中的斜率表示速度;v--t图中的斜率表示加速度 ,面积的物理意义v--t图中图象与坐标轴所围的面积表示位移。,画出几种典型运动的V-t图:
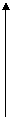 ①自由落体 ①自由落体
 ②竖直上抛 ②竖直上抛
③雨滴下落 ④汽车衡功率起动
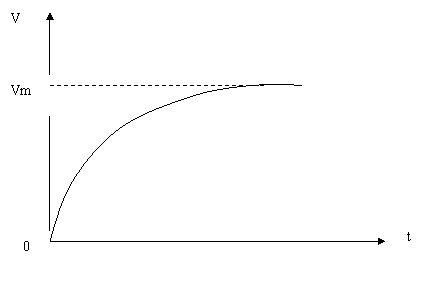
11.主要物理量及单位:初速度(Vo):m/s;加速度(a): m/s2 ;末速度( Vt ):m/s;时间(t)秒(s);位移(s):米(m);路程:米;速度单位换算:1m/s= 3.6 km/h。
注: (1)平均速度是矢量; (2)物体速度大,加速度不一定大; (3)a=(Vt-Vo)/t只是量度式,不是决定式; (4)高中物理中理想化模型有质点、光滑平面、点电荷、理想气体、弹簧振子等
⑸V与ΔV的相同点是 有相同的单位 不同点是 V是状态量,描述某时刻物体的运动状况,而ΔV是过程量,描述运动状态的改变情况。ΔV与a的相同点是 有相同的方向 不同点是ΔV表示速度改变了多少,而a表示速度的大小和方向改变的快慢程度
⑹平均速度与瞬时速度的关系是 时间间隔趋向于零 时的平均速度即为瞬时速度。速度与速率的关系是 速度即表示物体运动快慢又表明运动方向,是矢量;速率只表示物体运动快慢是标量。 速度与加速度的区别是速度描述物体运动状态,加速度描述运动状态改变的快慢 联系是加速度是速度的变化率,高中出现的几个变化率加速度是速度的变化率、速度是位移的变化率、力是动量的变化率、感应电动势是磁通量的变化率
⑺.其它相关内容:质点、位移和路程、参考系、时间与时刻、、相遇、追及。
2)自由落体运动
1.初速度Vo= 0
2.末速度Vt= gt
3.下落高度h= (从Vo位置向下计算) (从Vo位置向下计算)
4.推论 V2 =2gh
注: (1)自由落体运动是初速度为零的匀加速直线运动,遵循匀变速直线运动规律;
(2)a=g=9.8m/s2≈10m/s2(重力加速度在赤道附近较小,在高山处比平地小,方向竖直向下)。
(3)竖直上抛运动
1.位移s=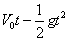
2.末速度Vt= V0-gt (g=9.8m/s2≈10m/s2)
3.有用推论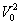 =-2gs =-2gs
4.上升最大高度Hm= (抛出点算起) (抛出点算起)
5.往返时间t= 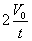 (从抛出落回原位置的时间) (从抛出落回原位置的时间)
注: (1)全过程处理:是匀减速直线运动,以向上为正方向,加速度取负值;
(2)分段处理:向上为匀减速直线运动,向下为自由落体运动,具有对称性;
(3)上升与下落过程具有对称性,如在同点速度等值反向等。
6.有恒定空气阻力的上抛:落回原地速度Vt < V0;上升时间 < 于下降时间;上升加速度的大小 > 于下降加速度大小,
(4)斜面上的运动(无其他外力)
1.光滑斜面上的加速度:a= gsinθ (斜面顷角θ,重力加速度g,)
2.有摩擦斜面上物体的加速度: a= g(sinθ- μcosθ)(斜面顷角θ,重力加速度g,摩擦因数μ)
二、质点的运动(二)----曲线运动、万有引力
⑴物体做直线运动的条件合力与速度在同一条直线上 物体做曲线运动的条件合力与速度不在同一条直线上
⑵匀速运动的两个特例匀速直线运动、匀速圆周运动 匀变速运动的两个特例匀变速直线运动、 平抛物体运动
⑶曲线运动的速度方向 时刻与轨迹相切,加速度方向 指向轨迹圆的圆心
 1)平抛运动 1)平抛运动
1.水平方向速度:Vx= V0
2.竖直方向速度:Vy= gt 速度增量ΔV= Vy= gt
3.水平方向位移:x= V0 t
4.竖直方向位移:y=
5.运动时间t=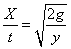
6.合速度Vt=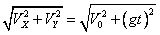 合速度方向与水平夹角β:tgβ= 合速度方向与水平夹角β:tgβ=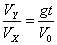
7.合位移:s= 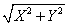 , 位移方向与水平夹角α:tgα= , 位移方向与水平夹角α:tgα=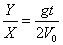
8.水平方向加速度:ax= 0 ;竖直方向加速度:ay= g
注: (1)平抛运动是匀变速曲线运动,加速度为g,通常可看作是水平方向的匀速直线运动与竖直方向的自由落体 运动的合成;
⑵运动时间由 下落高度决定与水平抛出速度无关;
⑶θ与β的关系为tgβ= 2 tgα;
⑷在平抛运动中时间t是解题关键;
⑸做曲线运动的物体必有加速度,当速度方向与所受合力(加速度)方向 不在同一条直线上 时,物体做曲线运动。
2)匀速圆周运动
1.线速度V=s/t= 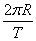
2.角速度ω=Φ/ t= 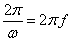
3.向心加速度a=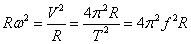
4.向心力F心=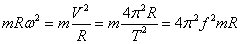 = F合 = F合
5.周期与频率:T=
6.角速度与线速度的关系:V=ωR
7.角速度与转速的关系ω=2πn (此处频率与转速意义相同,n的单位为转/秒)
8.主要物理量及单位:弧长(s):米(m);角度(Φ):弧度(rad);频率(f):赫(Hz);周期(T):秒(s);转速(n):r/s;半径(r):米(m);线速度(V):m/s;角速度(ω):rad/s;向心加速度:m/s2。
注:⑴半径转过Φ角,初速与末速夹角为 Φ 。转动过程中加速度a的方向时刻
指向圆心,加速度a与速度V的方向始终保持 垂直 。
⑵.角速度ω表示 半径转动的快慢 线速度V表示质点运动的快慢。
⑶向心力可以由某个具体力提供,也可以由合力提供,还可以由分力提供,方向始终与速度方向 垂直 ,指向 圆心 ;
⑷做 匀速圆周 运动的物体,其向心力等于合力,并且向心力只改变速度的 方向 ,不改变速度的大小,因此物体的动能保持不变,向心力不做功,但 动 量不断改变。
⑸变速圆周运动的物体合外力 不指向 圆心,可把这个力正交分解成向心的F向和切向的F切 ,F向的作用是改变 速度方向,F切 的作用是改变 速度大小。
⑹细绳拴小球在竖直面内做圆周运动的临界条件是 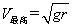 最高点与最低点绳子受拉力之差ΔT= 6 mg. 最高点与最低点绳子受拉力之差ΔT= 6 mg.
⑺物体做离心运动的条件是 :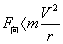
3)万有引力
1.开普勒第三定律:T2/R3=K=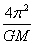 {R:轨道半径,T:周期,K:常量(与行星质量无关,取决于中心天体的质量)} {R:轨道半径,T:周期,K:常量(与行星质量无关,取决于中心天体的质量)}
2.万有引力定律:F= 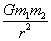 (G=6.67×10-11N•m2/kg2,方向在它们的连线上) (G=6.67×10-11N•m2/kg2,方向在它们的连线上)
3.天体上的重力和重力加速度:G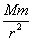 =mg; g=G =mg; g=G 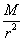 {R:天体半径(m),M:天体质量(kg)} {R:天体半径(m),M:天体质量(kg)}
4.卫星绕行速度、角速度、周期:V=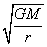 ;ω= ;ω=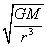 ;T=2π ;T=2π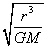
{M:中心天体质量}
5.第一宇宙速度V1=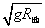 = =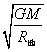 = 7。9km/s;第二宇宙速度V2= 11。2 km/s;第三宇宙速度V3=16。7 km/s = 7。9km/s;第二宇宙速度V2= 11。2 km/s;第三宇宙速度V3=16。7 km/s
6.地球同步卫星:①周期24小时 ②位置 赤道上空固定高度,③相对于地面上的观察者静止④高度h=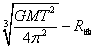 ≈36000km, ≈36000km,
注: (1)天体运动所需的向心力由万有引力提供,F向=F万;
(2)应用万有引力定律可估算天体的质量密度等;
(3)地球同步卫星只能运行于赤道上空,运行周期和地球自传周期相同;
(4)卫星轨道半径变小时,势能变 小、动能变 大、速度变大、周期变小;
(5)地球卫星的最大环绕速度和最小发射速度均为 7。9 km/s即 第一宇宙速度。
4)机械振动和机械波
1简谐振动,弹簧振子的振动过程:x=ACOSωt,v=Vm sinωt ,a=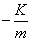 X X
2.单摆:回复力F= ,周期T= ,周期T= 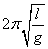 ,用单摆测重力加速度。 ,用单摆测重力加速度。
3.受迫振动频率特点:f=f驱动力
4.发生共振条件:f驱动力=f固,A=max,共振的防止和应用
5.机械波分类:横波、纵波
6.波速v=s/t=fλ= {波传播过程中,一个周期向前传播一个波长;波速大小由介质决定 {波传播过程中,一个周期向前传播一个波长;波速大小由介质决定
与振动无关,波由一种介质传播到另一种介质过程中频率不变}
7.声波的波速(在空气中)0℃:332m/s;20℃:344m/s;30℃:349m/s;(声波是纵波)
8.波发生明显衍射(波绕过障碍物或孔继续传播)条件:障碍物或孔的尺寸比波长小,或者 相当。
9.波的干涉条件:两列波频率相同(相差恒定、振幅相近、振动方向相同)
10.多普勒效应:由于波源与观测者间的相互运动,导致波源发射频率与接收频率不同{相互接近,接收频率升高,反之 降低。
注:(1)物体的固有频率与振幅、驱动力频率无关,取决于物体自身的因素;
(2)振动加强区是波峰与波峰或波谷与波谷相遇处,振动减弱区则是波峰与波谷相遇处; 若加强区某点A此时在波峰,经半个周期在波谷,经四分之一周期在平衡位置。
(3)波只是传播了振动,介质本身不随波发生迁移,是传递能量的一种方式;
(4)干涉与衍射是波特有的;
(5)振动图象与波动图象
三、力(常见的力、力的合成与分解)
1)常见的力
1.重力G=mg (方向竖直向下,g=9.8m/s2≈10m/s2,作用点在重心,适用于地球表面附近)
2.胡克定律F=-KX {方向沿恢复形变方向,k:劲度系数(N/m),x:形变量(m)}
3.滑动摩擦力F=mN ,
① N为接触面间的弹力,可以大于G;也可以等于G;也可以小于G
② m为滑动摩擦系数,与接触面材料和粗糙程度有关,与接触面积大小无关、与接触面相对运动快慢无关,与以及正压力N 无关.,与物体运动的速度无关
4.静摩擦力 : 由物体的平衡条件或牛顿第二定律求解,与正压力无关.
大小范围: 0≤f静≤ fm (fm为最大静摩擦力,与正压力有关)
说明:
a 、摩擦力可以与运动方向相同,也可以与运动方向相反,还可以与运动方向有一定夹角。 b、摩擦力可以作正功,也可以作 负功,还可以 不做功。
c、摩擦力的方向与物体间相对运动 的方向或 相对运动趋势的方向相反。
d、静止的物体可以受滑动摩擦力的作用,运动的物体可以受静摩擦力的作用
5.万有引力F=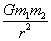 (G=6.67×10-11N•m2/kg2,方向在它们的连线上) (G=6.67×10-11N•m2/kg2,方向在它们的连线上)
6.静电力F=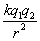 (k=9.0×109N•m2/C2,方向在它们的连线上) (k=9.0×109N•m2/C2,方向在它们的连线上)
7.电场力F=Eq (E:场强N/C,q:电量C,正电荷受的电场力与场强方向相同)
8.安培力F= ILB sinθ (θ为B与L的夹角,当L⊥B时:F=BIL,B//L时:F=0)
9.洛仑兹力f= q v b sinθ (θ为B与V的夹角,当V⊥B时:f=qVB,V//B时:f=0)
注: (1)劲度系数k由 弹簧本身因素 决定;
(2)摩擦因数μ与压力大小及接触面积大小无关,由接触面材料特性与表面状况等决定;
(3)fm略大于μFN,一般视为fm≈μFN;
(4)对“相对”的理解以摩擦力的施力物体为参照物,站到施力物体上看受力物体如何运动。
⑸安培力与洛仑兹力方向均用 右 手定则判定。
(6)物体的受力分析:①分析步骤确定研究对象 、先找场力再找接触力、 检查是否合理 ②检查是否 有多余力的力方法是每一个力都要有施力者 ③检查是否有漏掉方法是 每与一个物体接触都可能产生零到两个力
2)力的合成与分解
1.同一直线上力的合成同向:F=F1+F2, 反向:F=F1-F2 (F1>F2)
2.互成角度力的合成: F=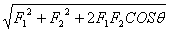 (余弦定理) (余弦定理)
F1⊥F2时: F= 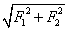
3.合力大小范围:ú F1-F2 ú ≤ F≤ F1 +F2
4.力的正交分解:Fx=Fcosβ,Fy=Fsinβ(β为合力与x轴之间的夹角tgβ=Fy/Fx)
注: (1)力(矢量)的合成与分解遵循平行四边形定则;
(2)合力与分力的关系是 等效替代 关系,可用合力替代分力的共同作用,反之也成立;
(3)除公式法外,也可用作图法求解,此时要选择标度,严格作图;
(4)F1与F2的值一定时,F1与F2的夹角(α角)越大,合力越 小
(5)同一直线上力的合成,可沿直线取正方向,用正负号表示力的方向,化简为代数运算。
(6)F1与F2夹角120 度时F1=F2=F合
四、动力学(运动和力)
1.牛顿第一运动定律(惯性定律):物体具有惯性,总保持 匀速直线运动或静止 状态,直到有 外力迫使它改变为止 。维持运动的原因是惯性 ,改变运动的原因是 受合外力 。描述运动的物理量是 速度。改变运动的方式有 只改变快慢(匀变速直线运动),只改变方向(匀速圆周运动),二者同时改变(平抛运动)。
2.牛顿第二运动定律:F合=ma。加速度a决定式是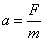 ,体现式是 ,体现式是 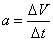 , ,
方向由 合外力 决定。即合力产生 加速度 , 加速度 改变速度。
理解(四性):(1)矢量性 (2)瞬时性 (3)独立性 (4) 同一性
3.牛顿第三运动定律:F=-F´{负号表示方向相反,实际应用:反冲运动}
① F、F´的三同 大小 、性质、作用时间,三不同 方向、效果、作用对象
②平衡力与作用力反作用力区别
③F、F´的作用效果间关系:做功两力的功不一定相等,冲量两力产生的冲量一定等大反向,加速度两力产生的加速度一定反向但不一定等大。
4.共点力的平衡F合=0,⑴推广 {正交分解法、}
⑵三力汇交原理、力的三角形:当物体受三个力平衡时,这三个力一定交与一点且组成封闭三角形
⑶动态平衡:当物体受三个力平衡而其中两个力缓慢变化时,这两个力的合力 一定与另一个力(例如重力)等大反向
④物体受三个力平衡时常用 三角形 法,物体受到四个以上力平衡时常用 正交分解法
5.超重:①超重失重的判断看加速度的方向,与速度 无关。
② 无论超重还是失重物体所受重力不变 ,超、失的只是支持力
③完全失重的两个典型例子是 自由落体、卫星绕地球的匀速圆周运动
④ 支持力FN>G时为 超 重,支持力FN<G时为 失重
6.牛顿定律的应用
⑴两种情况分析是 已知运动求力 、已知 力求运动,加速度是联系 运动和力的桥梁
⑵应用步骤是 确定研究对象、运动情况分析、受力分析、 列方程求解 、结果检验
⑶正交分解法应用;取加速度方向为X正方向则ΣFX= ma ΣFY= 0
五、功和能(功是能量转化的量度)
1.功:W=FSCOSα (定义式){W:功(J),F:恒力(N),s:位移(m),α:F、s间的夹角}
2.重力做功:Wab= mghab {m:物体的质量,g=9.8m/s2≈10m/s2,hab:a与b
高度差(hab=ha-hb)}
3.电场力做功:Wab= qUab{q:电量(C),Uab:a与b之间电势差(V)即Uab=φa-φb}
4.电功:W= UIt 普适式) {U:电压(V),I:电流(A),t:通电时间(s)}
5.功率:P=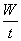 (定义式) {P:功率[瓦(W)],W:t时间内所做的功(J),t:做功所用时间(s)} (定义式) {P:功率[瓦(W)],W:t时间内所做的功(J),t:做功所用时间(s)}
6.汽车牵引力的功率:P= FV ;P平=Fv平 {P:瞬时功率,P平:平均功率}
7.汽车启动:①以恒定加速度启动,功率一定变化,匀加速的最大速度V1 < Vmax
②、以恒定功率启动,恒功率运动一定是 变 加速运动,某时刻加速度a=
③汽车最大行驶速度V max=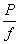
8.电功率:P= UI (普适式) {U:电路电压(V),I:电路电流(A)}
9.焦耳定律:Q= I2R t {Q:电热(J),I:电流强度(A),R:电阻值(Ω),t:通电时间(s)}
10.纯电阻电路中I=U/R;P=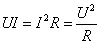 ;Q=W=UIt=U2t/R=I2Rt ;Q=W=UIt=U2t/R=I2Rt
11.动能:Ek=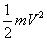 {Ek:动能(J),m:物体质量(kg),v:物体瞬时速度(m/s)} {Ek:动能(J),m:物体质量(kg),v:物体瞬时速度(m/s)}
12.重力势能:EP= mgh {EP :重力势能(J),g:重力加速度,h:竖直高度(m)(从零势能面起)}
13.电势能:EA=qφA{EA:带电体在A点的电势能(J),q:电量(C),φA:A点的电势(V)(从零势能面起)}
14.动能定理(对物体做正功,物体的动能增加): W合= W1 + W2 + W3 +```` 或W合=ΔEK
{W合:外力对物体做的总功,ΔEK:动能变化量,ΔEK=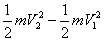 } }
15.机械能守恒定律:ΔE=0或EK1+EP1=EK2+EP2也可以是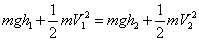
若只看系统的总势能变化和总动能变化:系统增加的动能等于势能减少量即ΔEK= -ΔEP ;
若系统内只有AB两个物体:A物体机械能增加量等于B物体机械能减少量即ΔEA=-ΔEB
匀强电场中准机械能守恒定律是 只有电场力做功时电势能与动能夺得总和不变
16.重力做功与重力势能的变化(重力做功等于物体重力势能 的 减少量)WG= -⊿EP
注: (1)功率大小表示做功快慢, 做功多少表示能量转化多少;
(2)O0≤α<90O 做正功;90O<α≤180O做负功;α=90o不做功(力的方向与位移(速度)方向垂直时该力不做功);
(3) 功是能量转化的量度
重力的功------量度------重力势能的变化 电场力的功-----量度------电势能的变化
分子力的功-----量度------分子势能的变化 合外力的功------量度-------动能的变化
重力(弹力、电场力、分子力)做正功,则重力(弹性、电、分子)势能
(4) 洛仑兹 力一定不做功; 重力 、 电场力做功与路径无关,
恒定大小的阻 力做功等于路程×力 。
(5)滑动摩擦力做功与机械能的变化关系 减少的机械能 等于滑动摩擦力与相对滑动路程的乘积 。系统内静摩擦力做的功不 改变系统的机械能。
(6)机械能守恒成立条件:只有重力和弹簧弹力做功其他力不做功,只是动能和势能之间的相互转化;
(7)判断机械能守恒的办法:①根据守恒条件看是否有重力以外的力做功,②根据机械能定义看 动能势能是否变化 ③根据能量转化看是否有其他能与机械能的转化
(8)能的其它单位换算:1kWh(度)= J,1eV=1。6×10-19 J; J,1eV=1。6×10-19 J;
* (9)弹簧弹性势能E=kx2/2,与劲度系数和形变量有关。
(10)验证机械能守衡与动量守衡实验
六、冲量与动量(物体的受力与动量的变化)
1.动量:p= mV {p:动量(kg/s),m:质量(kg),v:速度(m/s),方向与速度方向相同}
2.动量与动能的关系: P2= 2mEK ,区别:同一物体动量时矢量动能是标量,动量变化动能不一定变,动能变化动量一定改变
3.冲量:I= Ft {I:冲量(N•s),F:恒力(N),t:力的作用时间(s),方向由F决定}
4.动量定理:I= ⊿P 或Ft= mV2-mV1 {Δp:动量变化Δp=mvt–mvo,是矢量式}
5.动量守恒定律:p前总=p后总或p=p’´也可以是 m1V1+m2V2=m1v1´+m2v2´
6.弹性碰撞:Δp=0;ΔEk=0 {即系统动量和 动能均守恒}
7.非弹性碰撞Δp=0;0<ΔEK<ΔEKm {ΔEK:损失的动能,EKm:损失的最大动能}
8.完全非弹性碰撞Δp=0;ΔEK=ΔEKm {碰后 粘合在一起 机械能损失最 大 }
9.物体m1以v1初速度与静止的物体m2发生弹性正碰:
v1´= 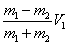 v2´= v2´=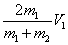
10.由9得的推论-----等质量弹性正碰时二者交换 速度 (动能守恒、动量守恒)
11.子弹m水平速度vo射入静止置于水平光滑地面的长木块M,并嵌入其中一起运动时的机械能损失 E损=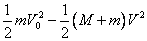 =fs相 =fs相
对 {vt:共同速度,f:阻力,s相对子弹相对长木块的位移}
注: (1)正碰又叫对心碰撞,速度方向在它们“中心”的连线上;
(2)以上表达式除动能外均为矢量运算,在一维情况下可取正方向化为代数运算;
(3)系统动量守恒的条件: 系统不受外力 或 系统内力远大于外力,则系统动量守恒(碰撞问题、爆炸问题、反冲问题等);
(4)碰撞过程(时间极短,发生碰撞的物体构成的系统)视为动量守恒,原子核衰变时动量守恒;
(5)爆炸过程视为动量守恒,这时化学能转化为动能,动能 增加 ;
(6)其它相关内容:反冲运动、火箭、航天技术的发展和宇宙航行。
七、分子动理论、能量守恒定律
1.阿伏加德罗常数NA=6.02×1023/mol;分子直径数量级 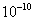 米 米
2.油膜法测分子直径d=V/s {V:单分子油膜的体积(m3),S:油膜表面积(m)2}
3.分子动理论内容:物质是由 大量分子组成的;大量分子做用不停息的热运动运动;分子间存 相互作用力。
4.分子间的引力和斥力(1)r>r0,f引>f斥,F分子力表现为引力 (2)r>10r0,f引=f斥≈0,F分子力≈0,E分子势能≈0 (3)r<r0,f引<f斥,F分子力表现为斥力
5.热力学第一定律 W + Q = DE
符号法则: 体积增大,气体对外做功,W为“一”;体积减小,外界对气体做功,W为“+”。气体从外界吸热,Q为“+”;气体对外界放热,Q为“-”。温度升高,内能增量DE是取“+”;温度降低,内能减少,DE取“一”。
三种特殊情况: ⑴ 等温变化 DE=0, 即 W+Q=0
⑵ 绝热膨胀或压缩:Q=0即 W=DE
⑶ 等容变化:W=0 ,Q=DE
{(做功和 热传递 ,这两种改变物体内能的方式,在效果上是等效的), W:外界对物体做的正功(J),Q:物体吸收的热量(J),ΔU:增加的内能(J),涉及到第一类永动机不可造出
6.热力学第二定律克氏表述:不可能使热量由低温物体传递到 高温物体,而不引起其它变化(热传导的方向性);开氏表述:不可能从单一热源吸收热量并把它全部用来做功,而不引起其它变化(机械能与内能转化的方向性)
7.热力学第三定律: 低温有极限{宇宙温度下限:零下273。15度(热力学零度)}
注: (1)布朗粒子不是 分子,布朗颗粒越小,布朗运动越 明显 ,温度越高 越剧烈;
(2)温度是分子平均动能的标志; (3)分子间的引力和斥力同时存在,随分子间距离的增大而 减小,但斥力比引力减小得更快
(4)分子力做正功,分子势能减小,在r0处F引=F斥且分子势能最小;(r0为分子处于平衡状态时分子间的距离;)
(5)气体膨胀,外界对气体做负功W﹤ 0;温度升高,内能 增大ΔU﹥0;吸收热量,Q﹥0
(6)物体的内能是指分子动能和分子势能的总和,对于理想气体分子间 无分子力,分子势能为零;
八、气体的性质
1.气体的状态参量:温度:宏观上,物体的冷热程度 ;微观上,物体内部分子无规则运动的剧烈程度的标志,热力学温度与摄氏温度关系:T= t+273 {T:热力学温度(K),t:摄氏温度(℃)}体积V:气体分子所能到达得空间,单位换算:1m3=103L= 106 mL 压强p:单位面积上,大量气体分子频繁撞击器壁而产生持续、均匀的压力,标准大气压:1atm=1.013×105Pa=76cmHg(1Pa=1N/m2)
2.气体分子运动的特点:分子间空隙大;除了碰撞的瞬间外,相互作用力极小可忽略不计;分子运动速率很大,平均速率可达几百米/秒
3.理想气体的状态方程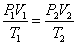 { {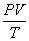 =恒量,T为热力学温度(K)} =恒量,T为热力学温度(K)}
注: (1)理想气体的内能与理想气体的体积无关,与温度和物质的量有关;
(2)公式成立条件均为一定质量的理想气体,使用公式时要注意温度的单位,t为摄氏温度(℃),而T为热力学温度(K)。 |

