2009年福建省初中学业考试大纲
(数 学)
一、命题依据
省教育厅制订的《2009年福建省初中学业考试大纲(数学)》。
二、命题原则
⒈体现数学课程标准的评价理念,有利于促进数学教学,全面落实《数学课程标准》所设立的课程目标;有利于改变学生的数学学习方式,提高学习效率;有利于高中阶段学校综合有效评价学生数学学习状况。
⒉重视对学生学习数学“双基”的结果与过程的评价,重视对学生数学思考能力和解决问题能力的发展性评价,重视对学生数学认识水平的评价。
⒊体现义务教育的性质,命题应面向全体学生,关注每个学生的发展。
⒋试题的考查内容、素材选取、试卷形式对每个学生而言要体现其公平性。制定科学合理的参考答案与评分标准,尊重不同的解答方式和表现形式。
⒌试题背景具有现实性。试题背景应来自学生所能理解的生活现实,符合学生所具有的数学现实和其他学科现实。
⒍试卷的有效性。关注学生学习数学结果与过程的考查,加强对学生思维水平与思维特征的考查。
中考试卷要有效发挥选择题、填空题、计算(求解)题、证明题、开放性问题、应用性问题、阅读分析题、探索性问题及其它各种题型的功能,试题设计必须与其评价的目标相一致。
试题的求解思考过程力求体现《数学课程标准》所倡导的数学活动方式,如观察、实验、猜测、验证、推理等等。
三、适用范围
全日制义务教育九年级学生初中数学学业考试。
四、考试范围
教育部颁发的《全日制义务教育数学课程标准(实验稿)》(7—9年级)中:数与代数、空间与图形、统计与概率、课题学习四个部分的内容。
五、内容和目标要求
⒈初中毕业生数学学业考试的主要考查方面包括:基础知识与基本技能;数学活动过程;数学思考;解决问题能力;对数学的基本认识等。
⑴基础知识与基本技能考查的主要内容
了解数产生的意义,理解代数运算的意义、算理,能够合理地进行基本运算与估算;能够在实际情境中有效地应用代数运算、代数模型及相关概念解决问题;能够借助不同的方法探索几何对象的有关性质;能够使用不同的方式表达几何对象的大小、位置与特征;能够在头脑里构建几何对象,进行几何图形的分解与组合,能对某些图形进行简单的变换;能够借助数学证明的方法确认数学命题的正确性;正确理解数据的含义,能够结合实际需要有效地表达数据特征,会根据数据结果作合理的预测;了解概率的涵义,能够借助概率模型、或通过设计活动解释一些事件发生的概率。
⑵“数学活动过程”考查的主要方面
数学活动过程中所表现出来的思维方式、思维水平,对活动对象、相关知识与方法的理解深度;从事探究与交流的意识、能力和信心等。
⑶“数学思考”方面的考查应当关注的主要内容
学生在数感与符号感、空间观念、统计意识、推理能力、应用数学的意识等方面的发展情况,其内容主要包括:
能用数来表达和交流信息;能够使用符号表达数量关系,并借助符号转换获得对事物的理解;能够观察到现实生活中的基本几何现象;能够运用图形形象来表达问题、借助直观进行思考与推理;能意识到作一个合理的决策需要借助统计活动去收集信息;面对数据时能对它的来源、处理方法和由此而得到的推测性结论作合理的质疑;面对现实问题时,能主动尝试从数学角度、用数学思维方法去寻求解决问题的策略;能通过观察、实验、归纳、类比等活动获得数学猜想,并寻求证明猜想的合理性;能合乎逻辑地与他人交流等等。
⑷“解决问题能力”考查的主要方面:
能从数学角度提出问题、理解问题、并综合运用数学知识解决问题;具有一定的解决问题的基本策略。
⑸“对数学的基本认识”考查的主要方面:
对数学内部统一性的认识(不同数学知识之间的联系、不同数学方法之间的相似性等);对数学与现实、或其他学科知识之间联系的认识等等。
⒉依据数学课程标准,考试要求的知识技能目标分为四个不同层次:了解(认识);理解;掌握;灵活运用。具体涵义如下:
了解(认识):能从具体事例中,知道或能举例说明对象的有关特征(或意义);能根据对象的特征,从具体情境中辨认出这一对象。
理解:能描述对象的特征和由来;能明确阐述此对象与有关对象之间的区别和联系。
掌握:能在理解的基础上,把对象运用到新的情境中。
灵活运用:能综合运用知识,灵活、合理地选择与运用有关的方法完成特定的数学任务。
数学活动水平的过程性目标分为三个不同层次:经历(感受);体验(体会);探索。具体涵义如下:
经历(感受):在特定的数学活动中,获得一些初步的经验。
体验(体会):参与特定的数学活动,在具体情境中初步认识对象的特征,获得一些经验。
探索:主动参与特定的数学活动,通过观察、实验、推理等活动发现对象的某些特征或与其它对象的区别和联系。
以下对《数学课程标准》中,数与代数、空间与图形、统计与概率、课题学习四个领域的具体考试内容与要求分述如下:
数 与 代 数
(一)数与式
⒈有理数
考试内容:
有理数,数轴,相反数,数的绝对值,有理数的加、减、乘、除、乘方,加法运算律,乘法运算律,简单的混合运算。
考试要求:
(1)理解有理数的意义,能用数轴上的点表示有理数,会比较有理数的大小。
(2)理解相反数和绝对值的意义,会求有理数的相反数与绝对值(绝对值符号内不含字母)。
(3)理解乘方的意义,掌握有理数的加、减、乘、除、乘方的运算法则、运算律、运算顺序以及简单的有理数的混合运算(以三步为主)。
(4)能用有理数的运算律简化有关运算,能用有理数的运算解决简单的问题。
⒉实数
考试内容:
无理数,实数,平方根,算术平方根,立方根,近似数和有效数字,
二次根式,二次根式的加、减、乘、除运算法则,简单的实数四则运算。
考试要求:
(1)了解平方根、算术平方根、立方根的概念,会用根号表示数的平方根、立方根。
(2)了解开方与乘方互为逆运算,会用平方运算求某些非负数的平方根,会用立方运算求某些数的立方根,会用科学计算器求平方根和立方根。
(3)了解无理数和实数的概念,知道实数与数轴上的点一一对应。
(4)能用有理数估计一个无理数的大致范围。
(5)了解近似数与有效数字的概念,会按要求求一个数的近似数,在解决实际问题中,能用计算器进行近似计算,并按问题的要求对结果取近似值。
(6)了解二次根式的概念及其加、减、乘、除运算法则,会用运算法则进行有关实数的简单四则运算(不要求分母有理化)。
⒊代数式
考试内容:
代数式,代数式的值,合并同类项,去括号。
考试要求:
(1)了解用字母表示数的意义。
(2)能分析简单问题的数量关系,并用代数式表示。
(3)能解析一些简单代数式的实际背景或几何意义。
(4)会求代数式的值;能根据特定的问题查阅资料,找到所需要的公式,并会代入具体的值进行计算。
(5)掌握合并同类项的方法和去括号的法则,能进行同类项的合并。
⒋整式与分式
考试内容:
整式,整式加减,整式乘除,整数指数幂,科学记数法。
乘法公式: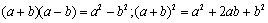 。 。
因式分解,提公因式法,公式法。
分式、分式的基本性质,约分,通分,分式的加、减、乘、除运算。
考试要求:
(1)了解整数指数幂的意义和基本性质,会用科学记数法表示数(包括在计算器上表示)。
(2)了解整式的概念,会进行简单的整式加、减运算;会进行简单的整式乘法运算(其中的多项式相乘仅指一次式相乘)。
(3)会推导乘法公式: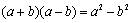 ; ;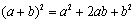 ,了解公式的几何背景,并能进行简单计算。 ,了解公式的几何背景,并能进行简单计算。
(4)会用提公因式法和公式法(直接用公式不超过两次)进行因式分解(指数是正整数)。
(5)了解分式的概念,掌握分式的基本性质,会利用分式的基本性质进行约分和通分,会进行简单的分式加、减、乘、除运算。
(二)方程与不等式
⒈方程与方程组
考试内容:
方程和方程的解,一元一次方程及其解法,一元二次方程及其解法,二元一次方程组及其解法,可化为一元一次方程的分式方程(方程中的分式不超过两个)。
考试要求:
(1)能够根据具体问题中的数量关系列出方程,体会方程是刻画现实世界的一个有效的数学模型。
(2)会用观察、画图或计算器等手段估计方程的解。
(3)会解一元一次方程、简单的二元一次方程组、可化为一元一次方程的分式方程(方程中的分式不超过两个)。
(4)理解配方法,会用因式分解法、公式法、配方法解简单的数字系数的一元二次方程。
(5)能根据具体问题的实际意义,检验方程的解的合理性。
⒉不等式与不等式组
考试内容:
不等式,不等式的基本性质,不等式的解集,一元一次不等式及其解法,一元一次不等式组及其解法。
考试要求:
(1)能够根据具体问题中的大小关系了解不等式的意义,掌握不等式的基本性质。
(2)会解简单的一元一次不等式,并能在数轴上表示出解集。会解由两个一元一次不等式组成的不等式组,并会用数轴确定解集。
(3)能够根据具体问题中的数量关系,列出一元一次不等式和一元一次不等式组,解决简单的问题。
(三)函数
⒈函数
考试内容:
平面直角坐标系,常量,变量,函数及其表示法。
考试要求:
(1)会从具体问题中寻找数量关系和变化规律。
(2)了解常量、变量、函数的意义,了解函数的三种表示方法,会用描点法画出函数的图象,能举出函数的实际例子。
(3)能结合图象对简单实际问题中的函数关系进行分析。
(4)能确定简单的整式、分式和简单实际问题中的函数的自变量取值范围,并会求出函数值。
(5)能用适当的函数表示法刻画某些实际问题中变量之间的关系。
(6)结合对函数关系的分析,尝试对变量的变化规律进行初步预测。
⒉一次函数
考试内容:
一次函数,一次函数的图象和性质,二元一次方程组的近似解。
考试要求:
(1)理解正比例函数、一次函数的意义,会根据已知条件确定一次函数表达式。
(2)会画一次函数的图象,根据一次函数的图象和解析式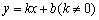 ,理解其性质(k>0或k<0时图象的变化情况)。 ,理解其性质(k>0或k<0时图象的变化情况)。
(3)能根据一次函数的图象求二元一次方程组的近似解。
(4)能用一次函数解决实际问题。
⒊反比例函数
考试内容:
反比例函数,反比例函数图象及其性质。
考试要求:
(1)理解反比例函数的意义,能根据已知条件确定反比例函数的表达式。
(2)能画出反比例函数的图象,根据图象和解析式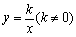 理解其性质(k>0或k<0时,图象的变化情况)。 理解其性质(k>0或k<0时,图象的变化情况)。
(3)能用反比例函数解决某些实际问题。
⒋二次函数
考试内容:
二次函数及其图象,一元二次方程的近似解。
考试要求:
(1)理解二次函数和抛物线的有关概念,能对实际问题情境的分析确定二次函数的表达式。
(2)会用描点法画出二次函数的图象,能结合图象认识二次函数的性质。
(3)会根据公式确定图象的顶点、开口方向和对称轴(公式不要求推导和记忆),并能解决简单的实际问题。
(4)会利用二次函数的图象求一元二次方程的近似解。
空 间 与 图 形
(一)图形的认识
⒈点、线、面,角。
考试内容:
点、线、面、角、角平分线及其性质。
考试要求:
(1)在实际背景中认识,理解点、线、面、角的概念。
(2)会比较角的大小,能估计一个角的大小,会计算角度的和与差,认识度、分、秒,会进行简单换算。
(3)掌握角平分线性质定理及逆定理。
⒉相交线与平行线
考试内容:
补角,余角,对顶角,垂线,点到直线的距离,线段垂直平分线及其性质,平行线,平行线之间的距离,两直线平行的判定及性质。
考试要求:
(1)了解补角、余角、对顶角的概念,知道等角的余角相等、等角的补角相等、对顶角相等。
(2)了解垂线、垂线段等概念,会用三角尺或量角器过一点画一条直线的垂线。了解垂线段最短的性质,理解点到直线距离的意义。
(3)知道过一点有且仅有一条直线垂直于已知直线。
(4)掌握线段垂直平分线性质定理及逆定理。
(5)了解平行线的概念及平行线基本性质,
(6)掌握两直线平行的判定及性质。
(7)会用三角尺和直尺过已知直线外一点画这条直线的平行线。
(8)体会两条平行线之间距离的意义,会度量两条平行线之间的距离。
⒊三角形
考试内容:
三角形,三角形的角平分线、中线和高,三角形中位线,全等三角形、全等三角形的判定,等腰三角形的性质及判定。等边三角形的性质及判定。直角三角形的性质及判定。勾股定理。勾股定理的逆定理。
考试要求:
(1)了解三角形有关概念(内角、外角、中线、高、角平分线),会画出任意三角形的角平分线、中线和高。
(2)掌握三角形中位线定理。
(3)了解全等三角形的概念,掌握两个三角形全等的判定定理。
(4)了解等腰三角形、直角三角形、等边三角形的有关概念,掌握等腰三角形、直角三角形、等边三角形的性质和判定定理;
(5)掌握勾股定理,会运用勾股定理解决简单问题;会用勾股定理的逆定理判定直角三角形。
⒋四边形
考试内容:
多边形,多边形的内角和与外角和,正多边形,平行四边形、矩形、菱形、正方形、梯形的概念和性质,平面图形的镶嵌。
考试要求:
(1)了解多边形的内角和与外角和公式,了解正多边形的概念。
(2)掌握平行四边形、矩形、菱形、正方形、梯形的概念和性质,了解它们之间的关系;了解四边形的不稳定性。
(3)掌握平行四边形、矩形、菱形、正方形、等腰梯形的有关性质和判定定理。
(4)了解线段、矩形、平行四边形、三角形的重心及物理意义(如一根均匀木棒、一块均匀的矩形木板的重心)。
(5)通过探索平面图形的镶嵌,知道任意一个三角形、四边形或正六边形可以镶嵌平面,并能运用这几种图形进行简单的镶嵌设计。
⒌圆
考试内容:
圆,弧、弦、圆心角的关系,点与圆、直线与圆以及圆与圆的位置关系,圆周角与圆心角的关系,三角形的内心和外心,切线的性质和判定,弧长,扇形的面积,圆锥的侧面积、全面积。
考试要求:
(1)理解圆及其有关概念,了解弧、弦、圆心角的关系,了解点与圆、直线与圆以及圆与圆的位置关系。
(2)了解圆的性质,了解圆周角与圆心角的关系、直径所对圆周角的特征。
(3)了解三角形的内心和外心。
(4)了解切线的概念、切线与过切点的半径之间的关系;能判定一条直线是否为圆的切线,会过圆上一点画圆的切线。
(5)会计算弧长及扇形的面积,会计算圆锥的侧面积和全面积。
⒍尺规作图
考试内容:
基本作图,利用基本作图作三角形,过一点、两点和不在同一直线上的三点作圆。
考试要求:
(1)能完成以下基本作图:作一条线段等于已知线段;作一个角等于已知角;作角的平分线;作线段的垂直平分线。
(2)能利用基本作图作三角形:已知三边作三角形;已知两边及其夹角作三角形;已知两角及其夹边作三角形;已知底边及底边上的高作等腰三角形。
(3)能过一点、两点和不在同一直线上的三点作圆。
(4)了解尺规作图的步骤,对于尺规作图题,会写已知、求作和作法(不要求证明)。
⒎视图与投影
考试内容:
简单几何体的三视图,直棱柱、圆锥的侧面展开图,视点、视角,盲区,投影。
考试要求:
(1)会画简单几何体(直棱柱、圆柱、圆锥、球)的三视图(主视图、左视图、俯视图)的示意图,会判断简单物体的三视图,能根据三视图描述基本几何体或实物原型。
(2)了解直棱柱、圆锥的侧面展开图,能根据展开图判断和制作立体模型。
(3)了解基本几何体与其三视图、展开图(球除外)之间的关系;知道这种关系在现实生活中的应用(如物体的包装)。
(4)了解并欣赏一些有趣的图形(如雪花曲线、莫比乌斯带)。
(5)知道物体阴影的形成,并能根据光线的方向辨认实物的阴影(如在阳光或灯光下,观察手的阴影或人的身影)。
(6)了解视点、视角及盲区的含义,能在简单的平面图和立体图中表示。
(7)了解中心投影和平行投影。
(二)图形与变换
⒈图形的轴对称、图形的平移、图形的旋转。
考试内容:
轴对称、平移、旋转。
考试要求:
(1)通过具体实例认识轴对称(或平移、旋转),探索它们的基本性质;
(2)能够按要求作出简单平面图形经过轴对称(或平移、旋转)后的图形,能作出简单平面图形经过一次或两次轴对称后的图形;
(3)探索基本图形(等腰三角形、矩形、菱形、等腰梯形、正多边形、圆)的轴对称(或平移、旋转)的性质及其相关性质。
(4)利用轴对称(或平移、旋转)及其组合进行图案设计;认识和欣赏轴对称(或平移、旋转)在现实生活中的应用。
⒉图形的相似
考试内容:
比例的基本性质,线段的比,成比例线段,图形的相似及性质,三角形相似的条件,图形的位似,锐角三角函数,30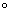 、45 、45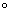 、60 、60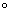 角的三角函数值。 角的三角函数值。
考试要求:
(1)了解比例的基本性质,了解线段的比、成比例线段,通过实例了解黄金分割。
(2)通过实例认识图形的相似,了解相似图形的性质,知道相似多边形的对应角相等,对应边成比例,面积的比等于对应边比的平方。
(3)了解两个三角形相似的概念,掌握两个三角形相似的条件。
(4)了解图形的位似,能够利用位似将一个图形放大或缩小。
(5)通过实例了解物体的相似,利用图形的相似解决一些实际问题(如利用相似测量旗杆的高度)。
(6)通过实例认识锐角三角函数(sinA,cosA, tanA),知道30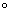 、45 、45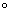 、60 、60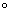 角的三角函数值;会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它对应的锐角。 角的三角函数值;会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它对应的锐角。
(7)运用三角函数解决与直角三角形有关的简单实际问题。
(三)图形与坐标
考试内容:
平面直角坐标系。
考试要求:
(1)认识并能画出平面直角坐标系;在给定的直角坐标系中,会根据坐标描出点的位置、由点的位置写出它的坐标。
(2)能在方格纸上建立适当的直角坐标系,描述物体的位置。
(3)在同一直角坐标系中,感受图形变换后点的坐标的变化。
(4)灵活运用不同的方式确定物体的位置。
(四)图形与证明
⒈了解证明的含义
考试内容:
定义、命题、逆命题、定理,定理的证明,反证法。
考试要求:
(1)理解证明的必要性。
(2)通过具体的例子,了解定义、命题、定理的含义,会区分命题的条件(题设)和结论。
(3)结合具体例子,了解逆命题的概念,会识别两个互逆命题,并知道原命题成立其逆命题不一定成立。
(4)理解反例的作用,知道利用反例可以证明一个命题是错误的。
(5)通过实例,体会反证法的含义。
(6)掌握用综合法证明的格式,体会证明的过程要步步有据。
⒉掌握证明的依据
考试内容:
一条直线截两条平行直线所得的同位角相等;
两条直线被第三条直线所截,若同位角相等,那么这两条直线平行;
若两个三角形的两边及其夹角分别相等,则这两个三角形全等;
两个三角形的两角及其夹边分别相等,则这两个三角形全等;
两个三角形的三边分别相等,则这两个三角形全等;
全等三角形的对应边、对应角分别相等。
考试要求:
运用以上6条“基本事实”作为证明命题的依据。
⒊利用2中的基本事实证明下列命题
考试内容:
(1)平行线的性质定理(内错角相等、同旁内角互补)和判定定理(内错角相等或同旁内角互补,则两直线平行)。
(2)三角形的内角和定理及推论(三角形的外角等于不相邻的两内角的和,三角形的外角大于任何一个和它不相邻的内角)。
(3)直角三角形全等的判定定理。
(4)角平分线性质定理及逆定理;三角形的三条角平分线交于一点(内心)。
(5)垂直平分线性质定理及逆定理;三角形的三边的垂直平分线交干一点(外心)。
(6)三角形中位线定理。
(7)等腰三角形、等边三角形、直角三角形的性质和判定定理。
(8)平行四边形、矩形、菱形、正方形、等腰梯形的性质和判定定理。
考试要求:
(1)会利用2中的基本事实证明上述命题。
(2)会利用上述定理证明新的命题。
(3)练习和考试中与证明有关的题目难度,应与上述所列的命题的论证难度相当。
⒋通过对欧几里得《原本》的介绍,感受几何的演绎体系对数学发展和人类文明的价值。
统 计 与 概 率
⒈统计
考试内容:
数据,数据的收集、整理、描述和分析。
抽样,总体,个体,样本。
扇形统计图。
加权平均数,数据的集中程度与离散程度,极差和方差。
频数、频率,频数分布,频数分布表、直方图、折线图。
样本估计总体,样本的平均数、方差,总体的平均数、方差。
统计与决策,数据信息,统计在社会生活及科学领域中的应用。
考试要求:
(1)会收集、整理、描述和分析数据,能用计算器处理较为复杂的统计数据。
(2)了解抽样的必要性,能指出总体、个体、样本。知道不同的抽样可能得到不同的结果。
(3)会用扇形统计图表示数据。
(4)理解并会计算加权平均数,能根据具体问题,选择合适的统计量表示数据的集中程度。
(5)会探索如何表示一组数据的离散程度,会计算极差与方差,并会用它们表示数据的离散程度。
(6)理解频数、频率的概念,了解频数分布的意义和作用。会列频数分布表,画频数分布直方图和频数折线图,并能解决简单的实际问题。
(7)体会用样本估计总体的思想,能用样本的平均数、方差来估计总体的平均数和方差。
(8)能根据统计结果做出合理的判断和预测,体会统计对决策的作用,能比较清晰地表达自己的观点,并进行交流。
(9)能根据问题查找相关资料,获得数据信息,会对日常生活中的某些数据发表自己的看法。
(10)能应用统计知识解决在社会生活及科学领域中一些简单的实际问题。
⒉概率
考试内容:
事件、事件的概率,列举法(包括列表、画树状图)计算简单事件的概率。
实验与事件发生的频率、大量重复实验与事件发生概率的估计。
运用概率知识解决实际问题。
考试要求:
(1)在具体情境中了解概率的意义,运用列举法(包括列表、画树状图)计算简单事件发生的概率。
(2)通过实验,获得事件发生的频率;知道大量重复实验时频率可作为事件发生概率的估计值。
(3)能运用概率知识解决一些实际问题。
课 题 学 习
考试内容:
课题的提出、数学模型、问题解决。
数学知识的应用、研究问题的方法。
考试要求:
(1)结合实际,会提出、探讨一些具有挑战性的研究课题,经历“问题情境—建立模型—求解—解释与应用”的基本过程。进而体验从实际问题抽象出数学问题、建立数学模型,综合应用已有的知识解决问题的过程。加深理解相关的数学知识,发展思维能力。
(2)体验数学知识之间的内在联系、初步形成对数学整体性的认识。
(3)理解数学知识在实际问题中的应用,初步掌握一些研究问题的方法与经验。
六、考试形式
初中毕业生数学学业考试采用闭卷笔试形式,全卷满分150分,考试时间120分钟。各地应重视现代信息技术在数学考试形式改革的作用,有条件的地方应积极利用现代信息技术设计考试形式。
七、试题难度
试题按其难度分为容易题、中档题和稍难题。难度值为0.70以上的试题为容易题,难度值为0.50~0.70之间的试题为中档题,难度值为0.30~0.50之间的试题为稍难题。全卷总体难度值为0.8左右。
八、试卷结构
试卷包含有填空题、选择题和解答题三种题型。三种题型的占分比例约为:填空题占25%,选择题占12.5%,解答题占62.5%。填空题只要求直接填写结果,不必写出计算过程或推证过程;选择题是四选一型的单项选择题;解答题包括计算题、证明题、应用题、作图题等,解答题应写出文字说明、演算步骤、推证过程或按题目要求正确作图。应设计结合现实情境的开放性、探索性问题,杜绝人为编造的繁难计算题和证明题。
全卷总题量(含小题)控制在25~30题,较为适宜。
九、试题示例
(一)填空题:
1.计算:|-3|=_______.(容易题)
 2.太阳半径大约是696000千米,用科学记数法表示为 _米.(容易题) 2.太阳半径大约是696000千米,用科学记数法表示为 _米.(容易题)
3.因式分解: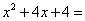 __________.(容易题) __________.(容易题)
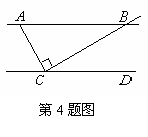
4.如图,AB∥CD,AC⊥BC,∠BAC=65°,则∠BCD=________度.(容易题)
5.“明天会下雨”是 事件.(填“必然”或“不可能”或“可能”) (容易题)
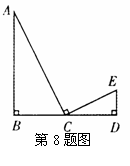
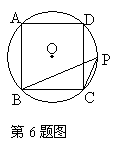
6.如图,正方形ABCD是⊙O的内接正方形,点P在劣弧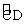 上不同于点C得到任意一点,则∠BPC的度数是_____________度.(容易题) 上不同于点C得到任意一点,则∠BPC的度数是_____________度.(容易题)
7.不等式组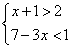 的解集是 _____________.(中档题) 的解集是 _____________.(中档题)
8.如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB=__________.(中档题)
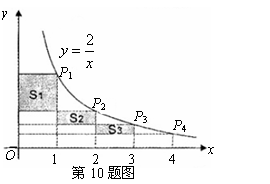 9.如图所示,课外活动中,小明在与旗杆AB距离为 9.如图所示,课外活动中,小明在与旗杆AB距离为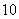 米的C处,用测角仪测得旗杆顶部A的仰角为 米的C处,用测角仪测得旗杆顶部A的仰角为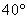 ,已知测角仪器的高CD= ,已知测角仪器的高CD=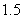 米,则旗杆AB的高是___________米.(精确到 米,则旗杆AB的高是___________米.(精确到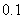 米)(中档题) 米)(中档题)
10.如图,在反比例函数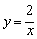 ( (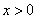 )的图象上,有点 )的图象上,有点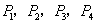 ,它们的横坐标依次为1,2,3,4.分别过这些点作 ,它们的横坐标依次为1,2,3,4.分别过这些点作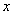 轴与 轴与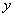 轴的垂线,图中所构成的阴影部分的面积从左到右依次为 轴的垂线,图中所构成的阴影部分的面积从左到右依次为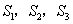 ,则 ,则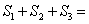 .(稍难题) .(稍难题)
(二)选择题:(A、B、C、D四个答案中有且只有一个是正确的)
11.下列各选项中,最小的实数是( ).
A.-3 B.-1 C.0 D.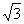 (容易题) (容易题)
12.下列运算正确的是( ).
A.x2+x3=2x5 B.(-2x)2·x3=4x5
C.(x-y)2=x2–y2 D.x3y2÷x2y3=xy(容易题)
13. 下列几何体,正(主)视图是三角形的是 ( ).
A. B. C. D.(容易题)
14.已知关于x的方程x2-px+q=0的两个根分别是0和-2,则p和q的值分别是( ).
A.p=-2,q=0 B.p=2,q=0
C.p=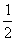 ,q=0 D.p=- ,q=0 D.p=-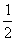 ,q=0 (中档题) ,q=0 (中档题)
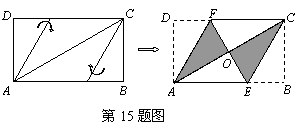 15.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为( ). 15.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为( ).
A.1 B.2
C.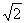 D. D.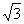 (中档题) (中档题)
16.如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均相等的结果,那么,小球最终到达H点的概率是( ).
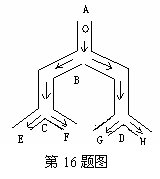 A. A.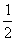 B. B.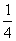
C.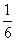 D. D.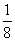 (中档题) (中档题)
17. 以边长为2厘米的正三角形的高为边长作第二个正三角形,以第二个正三角形的高为边长作第三个正三角形,以此类推,则第十个正三角形的边长是( ).
A.2×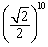 厘米 B.2× 厘米 B.2×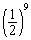 厘米 厘米
C.2×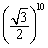 厘米 D.2× 厘米 D.2×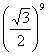 厘米(稍难题) 厘米(稍难题)
(三)解答题:
18.计算: |-2| + (4 - 7 )÷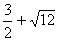 .(容易题) .(容易题)
19.先化简,再求值: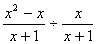 , 其中 , 其中 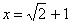 .(容易题) .(容易题)
20.如图,请在下列四个等式中,选出两个作为条件,推出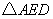 是等腰三角形,并予以证明.(写出一种即可) 是等腰三角形,并予以证明.(写出一种即可)
等式:①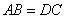 ,② ,②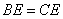 ,③ ,③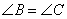 ,④ ,④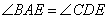 . .
 已知: 已知:
求证: 是等腰三角形. 是等腰三角形.
证明:(容易题)
21.有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况.
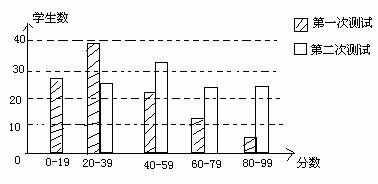
请你根据条形图提供的信息,回答下列问题(把答案填在题中横线上):
⑴两次测试最低分在第______次测试中;
⑵第_______次测试成绩较好;
⑶第一次测试中,中位数在_____分数段,第二次测试中,中位数在_____分数段.(容易题)
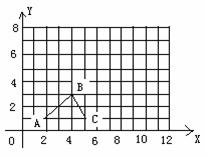
22.已知△ABC的三个顶点坐标如下表:
⑴将下表补充完整,并在直角坐标系中,画出△A/B/C/;
⑵观察△ABC与△A/B/C/,写出有关这两个三角形关系的一个正确结论.(容易题)
|
( x , y ) |
( 2x , 2y ) |
|
A ( 2 , 1 ) |
A/ ( 4 , 2 ) |
|
B ( 4 , 3 ) |
B/ ( , ) |
|
C ( 5 , 1 ) |
C/ ( , ) |
23.某商店购进一种商品,单价30元.试销中发现这种商品每天的销售量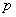 (件)与每件的销售价 (件)与每件的销售价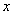 (元)满足关系: (元)满足关系: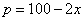 .若商店每天销售这种商品要获得200元的利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?(中档题) .若商店每天销售这种商品要获得200元的利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?(中档题)
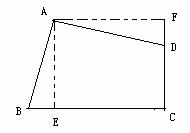
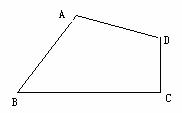 24.如图,在四边形ABCD中,∠A=90°,∠ABC与∠ADC互补. 24.如图,在四边形ABCD中,∠A=90°,∠ABC与∠ADC互补.
⑴求∠C的度数;
⑵若BC>CD且AB=AD,请在图上画出一条线段,把四边形ABCD分成两部分,使得这两部分能够重新拼成一个正方形,并说明理由;
⑶若CD=6,BC=8,S四边形ABCD=49,求AB的值. (中档题)
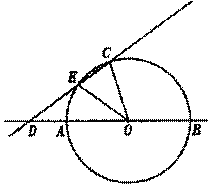 25.如图,AB是⊙O的直径,点C在⊙O上,∠BOC=108°,过点C作直线CD分别交直线AB和⊙O于点D、E,连接OE,DE= 25.如图,AB是⊙O的直径,点C在⊙O上,∠BOC=108°,过点C作直线CD分别交直线AB和⊙O于点D、E,连接OE,DE=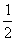 AB,OD=2 . AB,OD=2 .
⑴求∠CDB的度数;
⑵我们把有一个内角等于36°的等腰三角形称为黄金三角形.它的腰长与底边长的比(或者底边长与腰长的比)等于黄金分割比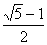 . .
①求弦CE的长;
②在直线AB或CD上是否存在点P(点C、D除外),使△POE是黄金三角形?若存在,画出点P,简要说明画出点P的方法(不要求证明);若不存在,说明理由.(稍难题)
26.如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒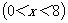 ,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米. ,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
⑴求y1与x的函数关系,并在图2中画出y1的图象;
⑵如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;
⑶在图2中,点G是x轴正半轴上一点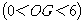 ,过G作EF垂直于x轴,分别交y1、y2的图象于点E、F. ,过G作EF垂直于x轴,分别交y1、y2的图象于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.(稍难题)
参考答案
一、1.3; 2.6.96×108; 3.(x+2)2; 4.25; 5.可能;
6.45; 7.x>2; 8.4; 9.9.9; 10.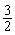 ; ;
二、11.A;12.B;13.C;14.A;15.D;16.B;17.D;
三、18.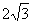 ; ;
19.解:原式=x-1,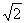 ; ;
20.已知:①③(或①④,或②③,或②④)(3分)
证明:在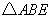 和 和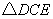 中, 中,
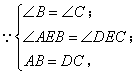
 . .
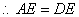 . .
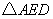 是等腰三角形. 是等腰三角形.
21. 解:(1)一;(2)二;(3)20~39,40~59;
22.解:(1)B/(8,6),C/(10,2),图略;
(2)如:△ABC∽△A/B/C/.
23.解:根据题意得: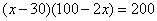 , ,
整理得: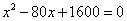
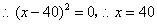 (元) (元)
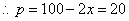 (件) (件)
答:每件商品的售价应定为40元,每天要销售这种商品20件.
 24.解:(1)∵∠ABC与∠ADC互补, 24.解:(1)∵∠ABC与∠ADC互补,
∴∠ABC+∠ADC=180°.
∵∠A=90°,
∴∠C=360°-90°-180°=90°.
(2)过点A作AE⊥BC,垂足为E.
则线段AE把四边形ABCD分成△ABE和四边形AECD两部分,把△ABE以A点为旋转中心,逆时针旋转90°,则被分成的两部分重新拼成一个正方形.
过点A作AF∥BC交CD的延长线于F,
∵∠ABC+∠ADC=180°,又∠ADF+∠ADC=180°,
∴∠ABC=∠ADF.
∵AD=AB,∠AEC=∠AFD=90°,∴△ABE≌△ADF.
 ∴AE=AF.∴四边形AECF是正方形. ∴AE=AF.∴四边形AECF是正方形.
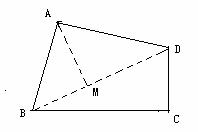
(3)解法1:连结BD,
∵∠C=90°,CD=6,BC=8, BCD中, BCD中,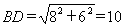 . .
又∵S四边形ABCD=49,∴S△ABD=49-24=25.
过点A作AM⊥BD垂足为M,
∴S△ABD=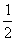 ×BD×AM=25.∴AM=5. ×BD×AM=25.∴AM=5.
又∵∠BAD=90°,∴△ABM∽△ABD.
∴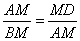 . .
设BM=x,则MD=10-x,
∴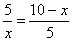 .解得x=5. .解得x=5.
∴AB=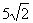 . .
解法2:连结BD,∠A=90°.
设AB=x,BD=y,则x2+y2=102,①
∵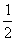 xy=25,∴xy=50.② xy=25,∴xy=50.②
由①,②得:(x–y)2=0.
∴x=y.
2x2=100.
∴x=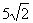 . .
25.解:(1)∵AB是⊙O的直径,DE=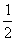 AB, AB,
∴OA=OC=OE=DE.
则∠EOD=∠CDB, ∠OCE=∠OEC.
设∠CDB=x,则∠EOD=x,∠OCE=∠OEC=2x.
 又∠BOC=108°,∴∠CDB+∠OCD=108°. 又∠BOC=108°,∴∠CDB+∠OCD=108°.
∴x+2x=108,x=36°. ∴∠CDB=36°.
(2)①∵∠COB=108°,∴∠COD=72°.
又∠OCD=2x=72°,
∴∠OCD=∠COD.∴OD=CD.
∴△COD是黄金三角形.
∴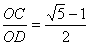 . .
∵OD=2,∴OC=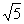 -1, -1,
∵CD=OD=2,DE=OC=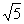 -1, -1,
∴CE=CD-DE=2-(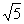 -1)=3- -1)=3-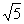 . .
②存在,有三个符合条件的点P1、P2、P3(如图所示).
ⅰ)以OE为底边的黄金三角形:作OE的垂直平分线分别交直线AB、CD得到点P1、P2 .
ⅱ)以OE为腰的黄金三角形:点P3与点A重合.
26.解:⑴∵ ,CD=3,CQ=x, ,CD=3,CQ=x,
 ∴ ∴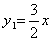 . .
图象如图所示.
⑵方法一:
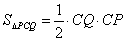 ,CP=8k-xk,CQ=x, ,CP=8k-xk,CQ=x,
∴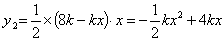 . .
∵抛物线顶点坐标是(4,12),
∴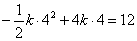 .解得 .解得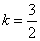 . .
则点P的速度每秒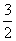 厘米,AC=12厘米. 厘米,AC=12厘米.
方法二:
观察图象知,当x=4时,△PCQ面积为12.
此时PC=AC-AP=8k-4k=4k,CQ=4.
∴由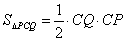 ,得 ,得 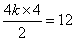 .解得 .解得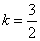 . .
则点P的速度每秒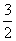 厘米,AC=12厘米. 厘米,AC=12厘米.
方法三:
设y2的图象所在抛物线的解析式是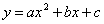 . .
∵图象过(0,0),(4,12),(8,0),
∴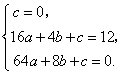 解得 解得 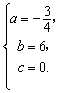
∴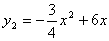 . ① . ①
∵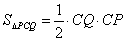 ,CP=8k-xk,CQ=x, ,CP=8k-xk,CQ=x,
∴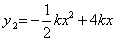 . ② . ②
比较①②得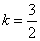 . .
则点P的速度每秒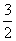 厘米,AC=12厘米. 厘米,AC=12厘米.
⑶①观察图象,知
线段的长EF=y2-y1,表示△PCQ与△DCQ的面积差(或△PDQ面积).
②由⑵得 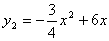 .(方法二, .(方法二,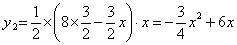 ) )
∵EF=y2-y1,
∴EF=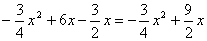 , ,
∵二次项系数小于0,
∴在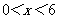 范围,当 范围,当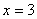 时, 时,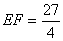 最大. 最大. |

