|
本试卷满分150分,考试时间120分钟
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个备选项中,只有一项是符合题目要求的。
1. 设全集U=R,集合M={x|x≤1或x≥3},集合P=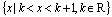 ,且UM ,且UM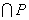 ≠ ≠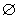 ,则实数k的取值范围是( ) ,则实数k的取值范围是( )
A. 0<k<3 B. k≤0 或k≥3 C. k<3 D. k>0
2. 设a∈R,且(a+i)2i为正实数,则a=( )
A. 1 B. 0 C. -1 D. 0或-1
3.“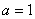 ”是“函数 ”是“函数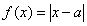 在区间 在区间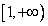 上为增函数”的( ) 上为增函数”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4. 已知等差数列{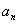 }的前n项和为 }的前n项和为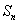 ,若 ,若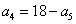 ,则 ,则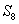 =( ) =( )
A. 68 B. 72 C. 54 D. 90
5.定义在R上的函数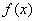 ,如果存在函数 ,如果存在函数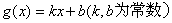 ,使得 ,使得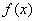 ≥ ≥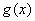 对一切实数 对一切实数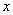 都成立,则称 都成立,则称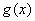 为函数 为函数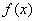 的一个承托函数.现有如下命题: 的一个承托函数.现有如下命题:
① 对给定的函数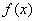 ,其承托函数可能不存在,也可能有无数个; ,其承托函数可能不存在,也可能有无数个;
② 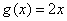 为函数 为函数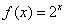 的一个承托函数; 的一个承托函数;
③定义域和值域都是R的函数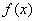 不存在承托函数. 不存在承托函数.
其中正确命题的序号是( )
(A) ① (B) ② (C) ①③ (D) ②③
6. 设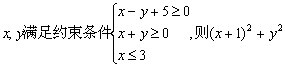 的最大值为( ) 的最大值为( )
A. 80 B. 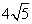 C. 25 D. C. 25 D.  |

