|
数 学
一、命题依据
以教育部制定的《全日制义务教育数学课程标准(实验稿)》(以下简称《标准》)和福建省教育厅颁发的《2009年福建省初中学业考试大纲(数学)》为依据,结合我市初中数学教学实际进行命题.
二、命题原则
1、体现《标准》的评价理念,有利于促进数学教学,全面落实《标准》所设立的课程目标;有利于改变学生的数学学习方式,激励学生的学习热情,促进学生的全面发展;有利于高中阶段学校综合有效评价学生数学学习状况.
2、遵循《标准》的基本理念,以第三学段(7—9年级)的知识与技能目标为基准,恰当考察学生对基础知识与基本技能的理解和掌握程度.
3、关注学生学习数学“双基”的结果与过程,重视对学生数学思考能力和解决问题能力的发展性评价,加强对学生数学认识水平与思维特征的考查.
4、试题的考查内容、素材选取、试卷形式对每个学生而言要体现其公平性.制定科学合理的参考答案与评分标准,尊重不同的解答方式和表现形式.
5、应设计结合现实背境的试题,以考查学生对数学知识的理解和运用所学知识解决问题的能力.试题背景应来自学生所能理解的生活现实,符合学生所具有的数学现实和其他学科现实.
6、要有效发挥选择题、填空题、计算(求解)题、证明题、应用性问题、探索性问题、开放性问题及其它各种题型的功能,试题设计必须与其评价的目标相一致,不出偏题、怪题和死记硬背的题目.
三、适用范围
全日制义务教育九年级学生初中数学学业考试.
四、考试范围
《标准》第三学段(7—9年级)中“数与代数”、“空间与图形”、“统计与概率”、“实践与综合应用(课题学习)”等四个领域的内容.
五、内容和目标要求
1、初中毕业生数学学业考试的主要考查方面包括:基础知识与基本技能;数学活动过程;数学思考;解决问题的能力;对数学的基本认识等。
(1)“基础知识与基本技能”考查的主要内容:
能将一些实际问题抽象成“数与代数”问题,掌握“数与代数”的基础知识与基本技能,并能解决简单的问题;能探究物体与图形的形状、大小、位置关系和变换过程,掌握“空间与图形”的基础知识与基本技能,并能解决简单的问题;能提出问题,收集和处理数据、作出决策和预测,掌握“统计与概率”的基础知识与基本技能,并能解决简单的问题.
(2)“数学活动过程”考查的主要方面:
数学活动过程中所表现出来的思维方式、思维水平,对活动对象、相关知识与方法的理解深度;从事探究与交流的意识、能力和信心等.
(3)“数学思考”方面的考查应当关注的主要内容:
学生在数感与符号感、空间观念、统计意识、推理能力、应用数学的意识等方面的发展情况. 其内容主要包括:
能用数来表达和交流信息;能够使用符号表达数量关系,并借助符号转换获得对事物的理解;能够观察到现实生活中的基本几何现象;能够运用图形形象来表达问题、借助直观进行思考与推理;能意识到作一个合理的决策需要借助统计活动去收集信息;面对数据时能对它的来源、处理方法和由此而得到的推测性结论作合理的质疑;面对现实问题时,能主动尝试从数学角度、用数学思维方法去寻求解决问题的策略;能通过观察、实验、归纳、类比等活动获得数学猜想,并寻求证明猜想的合理性;能合乎逻辑地与他人交流等等.
(4)“解决问题的能力”考查的主要方面:
能从数学角度提出问题、理解问题、并能综合运用所学知识与技能解决问题,具
有一定的解决问题的基本策略.
(5)“对数学的基本认识”考查的主要方面:
对数学内部统一性的认识(不同数学知识之间的联系、不同数学方法之间的相似性等);对数学与现实、或其他学科知识之间联系的认识等等.
2、依据《标准》,考查要求的知识技能目标分成四个不同层次:了解(认识);理解;掌握;灵活运用.具体涵义如下:
了解(认识):能从具体事例中,知道或能举例说明对象的有关特征(或意义);能根据对象的特征,从具体情境中辨认出这一对象.
理解:能描述对象的特征和由来;能明确地阐述此对象与有关对象之间的区别和联系.
掌握:能在理解的基础上,把对象运用到新的情境中.
灵活运用:能综合运用知识,灵活、合理地选择与运用有关的方法完成特定的数学任务.
数学活动水平的过程性目标分成三个不同层次:经历(感受);体验(体会);探索.具体涵义如下:
经历(感受):在特定的数学活动中,获得一些初步的经验.
体验(体会):参与特定的数学活动,在具体情境中初步认识对象的特征,获得一些经验.
探索:主动参与特定的数学活动,通过观察、实验、推理等活动发现对象的某些特征或与其他对象的区别和联系.
以下对《标准》中,数与代数、空间与图形、统计与概率、课题学习四个领域的具体考试内容与要求分述如下:
(一)数与代数
1、数与式
(1)有理数
考试内容:
有理数,数轴,相反数,数的绝对值.有理数的加、减、乘、除、乘方,加法、乘法运算律,有理数简单的混合运算.
考试要求:
①理解有理数的意义,能用数轴上的点表示有理数,会比较有理数的大小.
②借助数轴理解相反数和绝对值的意义,会求有理数的相反数与绝对值(绝对值符号内不含字母).
③理解乘方的意义,掌握有理数的加、减、乘、除、乘方及简单的混合运算(以三步为主).
④理解有理数的运算律,并能运用运算律简化运算.
⑤能运用有理数的运算解决简单的问题.
⑥能对含有较大数字的信息作出合理的解释和推断.
(2)实数
考试内容:
平方根,算术平方根,立方根.无理数,实数.近似数与有效数字.
二次根式,二次根式的加、减、乘、除.实数的简单四则运算.
考试要求:
①了解平方根、算术平方根、立方根的概念,会用根号表示数的平方根、立方根.
②了解开方与乘方互为逆运算,会用平方运算求某些非负数的平方根.会用立方运算求某些数的立方根,会用计算器求平方根和立方根.
③了解无理数和实数的概念,知道实数与数轴上的点一一对应.
④能用有理数估计一个无理数的大致范围.
⑤了解近似数与有效数字的概念,在解决实际问题中,能用计算器进行近似计算,并按问题的要求对结果取近似值.
⑥了解二次根式的概念及其加、减、乘、除运算法则,会用它们进行有关实数的简单四则运算(不要求分母有理化).
(3)代数式
考试内容:
代数式,代数式的值.
考试要求:
①理解用字母表示数的意义.
②能分析简单问题的数量关系,并用代数式表示.
③能解释一些简单代数式的实际背景或几何意义.
④会求代数式的值;能根据特定的问题查阅资料,找到所需要的公式,并会代入具体的值进行计算.
(4)整式与分式
考试内容:
整式,整式的加减法,整式乘除,整数指数幂,科学记数法.
乘法公式: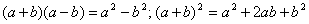 . .
因式分解,提公因式法,公式法.
分式、分式的基本性质,分式的约分、通分,简单的分式加、减、乘、除运算.
考试要求:
①了解整数指数幂的意义和基本性质,会用科学记数法表示数(包括在计算器上表示).
②了解整式的概念,会进行简单的整式加、减运算;会进行简单的整式乘法运算(其中的多项式相乘仅指一次式相乘).
③会推导乘法公式: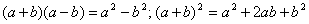 ,了解公式的几何背景,并能进行简单计算. ,了解公式的几何背景,并能进行简单计算.
④会用提公因式法、公式法(直接用公式不超过二次)进行因式分解(指数是正整数).
⑤了解分式的概念,会利用分式的基本性质进行约分和通分,会进行简单的分式加、减、乘、除运算.
2、方程与不等式
(1)方程与方程组
考试内容:
方程和方程的解,一元一次方程及其解法和应用,二元一次方程组及其解法和应用,一元二次方程及其解法和应用,可化为一元一次方程的分式方程(方程中的分式不超过两个).
考试要求:
①能够根据具体问题中的数量关系列出方程,体会方程是刻画现实世界的一个有效的数学模型.
②会用观察、画图或计算器等手段估计方程的解.
③会解一元一次方程、简单的二元一次方程组、可化为一元一次方程的分式方程(方程中的分式不超过两个).
④理解配方法,会用因式分解法、公式法、配方法解简单的数字系数的一元二次方程.
⑤能根据具体问题的实际意义,检验方程的解的合理性.
(2)不等式与不等式组
考试内容:
不等式,不等式的基本性质,不等式的解集,一元一次不等式及其解法和应用,一元一次不等式组及其解法.
考试要求:
①能够根据具体问题中的大小关系了解不等式的意义,掌握不等式的基本性质.
②会解简单的一元一次不等式,并能在数轴上表示出解集.会解由两个一元一次不等式组成的不等式组,并会用数轴确定解集.
③能够根据具体问题中的数量关系,列出一元一次不等式解决简单的问题.
3、函数
(1)函数
考试内容:
常量,变量,函数及其表示法.
考试要求:
①会探索具体问题中的数量关系和变化规律.
②了解常量、变量的意义,了解函数的概念和三种表示方法,能举出函数的实际例子.
③能结合图象对简单实际问题中的函数关系进行分析.
④能确定简单的整式、分式和简单实际问题中的函数的自变量取值范围,并会求出函数值.
⑤能用适当的函数表示法刻画某些实际问题中变量之间的关系.
⑥结合对函数关系的分析,尝试对变量的变化规律进行初步预测.
(2)一次函数
考试内容:
一次函数,一次函数的图象和性质,二元一次方程组的近似解.
考试要求:
①理解正比例函数、一次函数的意义,会根据已知条件确定一次函数表达式.
②会画一次函数的图象,根据一次函数的图象和解析式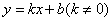 理解其性质( 理解其性质(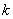 >0或 >0或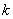 <0时图象的变化情况). <0时图象的变化情况).
③能根据一次函数的图象求二元一次方程组的近似解.
④能用一次函数解决实际问题.
(3)反比例函数
考试内容:
反比例函数,反比例函数图象及其性质.
考试要求:
①理解反比例函数的意义,能根据已知条件确定反比例函数表达式.
②能画出反比例函数的图象,根据图象和解析式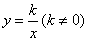 理解其性质( 理解其性质(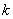 >0或 >0或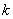 <0时图象的变化). <0时图象的变化).
③能用反比例函数解决某些实际问题.
(4)二次函数
考试内容:
二次函数及其图象,一元二次方程的近似解.
考试要求:
①通过对实际问题情境的分析确定二次函数的表达式,并体会二次函数的意义.
②会用描点法画出二次函数的图象,能从图象上认识二次函数的性质.
③会根据公式确定图象的顶点、开口方向和对称轴(公式不要求记忆和推导),并能解决简单的实际问题.
④会利用二次函数的图象求一元二次方程的近似解.
(二)空间与图形
1、图形的认识
(1)点、线、面、角.
考试内容:
点、线、面、角、角平分线及其性质.
考试要求:
①在实际背景中认识,理解点、线、面、角的概念.
②会比较角的大小,能估计一个角的大小,会计算角度的和与差,认识度、分、秒,会进行简单换算.
③了解角平分线及其性质.
(2)相交线与平行线
考试内容:
补角,余角,对顶角,垂线,点到直线的距离,线段垂直平分线及其性质,平行线,平行线之间的距离,两直线平行的判定及性质.
考试要求:
①了解补角、余角、对顶角,知道等角的余角相等、等角的补角相等、对顶角相等.
②了解垂线、垂线段等概念,了解垂线段最短的性质,体会点到直线距离的意义.
③知道过一点有且仅有一条直线垂直于已知直线,会用三角尺或量角器过一点画一条直线的垂线.
④了解线段垂直平分线及其性质.
⑤了解平行线的概念及平行线基本性质.掌握两直线平行的判定及性质.
⑥掌握两直线平行的判定及性质.
⑦会用三角尺和直尺过已知直线外一点画这条直线的平行线.
⑧体会两条平行线之间距离的意义,会度量两条平行线之间的距离.
(3)三角形
考试内容:
三角形,三角形的角平分线、中线和高,三角形中位线,全等三角形,全等三角形的判定,等腰三角形的性质及判定,等边三角形的性质及判定,直角三角形的性质及判定,勾股定理,勾股定理的逆定理.
考试要求:
①了解三角形有关概念(内角、外角、中线、高、角平分线),会画出任意三角形的角平分线、中线和高,了解三角形的稳定性.
②掌握三角形中位线的性质.
③了解全等三角形的概念,掌握两个三角形全等的条件.
④了解等腰三角形、等边三角形、直角三角形的有关概念,掌握等腰三角形、等边三角形、直角三角形的性质,掌握一个三角形是等腰三角形、等边三角形、直角三角形的条件.
⑤掌握勾股定理,会运用勾股定理解决简单问题;会用勾股定理的逆定理判定直角三角形.
(4)四边形
考试内容:
多边形,多边形的内角和与外角和,正多边形,平行四边形、矩形、菱形、正方形、梯形的概念及性质.平面图形的镶嵌.
考试要求:
①了解多边形的内角和与外角和公式,了解正多边形的概念.
②掌握平行四边形、矩形、菱形、正方形、梯形的概念和性质,了解它们之间的关系;了解四边形的不稳定性.
③掌握平行四边形、矩形、菱形、正方形、等腰梯形的有关性质,掌握四边形是平行四边形、矩形、菱形、正方形、等腰梯形的条件.
④探索并了解线段、矩形、平行四边形、三角形的重心及物理意义.
⑤通过探索平面图形的镶嵌,知道任意一个三角形、四边形或正六边形可以镶嵌平面,并能运用这几种图形进行简单的镶嵌设计.
(5)圆
考试内容:
圆,弧、弦、圆心角的关系,点与圆、直线与圆以及圆与圆的位置关系,圆周角与圆心角的关系,三角形的内心和外心,切线的性质和判定,弧长及扇形的面积,圆锥的侧面积、全面积.
考试要求:
①理解圆及其有关概念,了解弧、弦、圆心角的关系,了解点与圆、直线与圆以及圆与圆的位置关系.
②了解圆的性质,了解圆周角与圆心角的关系、直径所对圆周角的特征.
③了解三角形的内心和外心.
④了解切线的概念、切线与过切点的半径之间的关系;能判定一条直线是否为圆的切线,会过圆上一点画圆的切线.
⑤会计算弧长及扇形的面积,会计算圆锥的侧面积和全面积.
(6)尺规作图
考试内容:
基本作图,利用基本作图作三角形,过一点、两点和不在同一直线上的三点作圆.
考试要求:
①能完成以下基本作图:作一条线段等于已知线段,作一个角等于已知角,作角的平分线,作线段的垂直平分线.
②能利用基本作图作三角形:已知三边作三角形;已知两边及其夹角作三角形;已知两角及其夹边作三角形;已知底边及底边上的高作等腰三角形.
③能过一点、两点和不在同一直线上的三点作圆.
④了解尺规作图的步骤,对于尺规作图题,会写已知、求作和作法(不要求证明).
(7)视图与投影
考试内容:
简单几何体的三视图,直棱柱、圆锥的侧面展开图.
考试要求:
①会画基本几何体(直棱柱、圆柱、圆锥、球)的三视图(主视图、左视图、俯视图),会判断简单物体的三视图,能根据三视图描述基本几何体或实物原型.
②了解直棱柱、圆锥的侧面展开图,能根据展开图判断和制作立体模型.
③了解基本几何体与其三视图、展开图(球除外)之间的关系;知道这种关系在现实生活中的应用(如物体的包装).
④观察与现实生活有关的图片(如照片、简单的模型图、平面图、地图等),了解并欣赏一些有趣的图形(如雪花曲线等).
2、图形与变换
(1)图形的轴对称、图形的平移、图形的旋转
考试内容:
轴对称、平移、旋转.
考试要求:
①通过具体实例认识轴对称(或平移、旋转),探索它们的基本性质.
②能够按要求作出简单平面图形经过轴对称(或平移、旋转)后的图形,能作出简单平面图形经过一次或两次轴对称后的图形.
③探索基本图形(等腰三角形、矩形、菱形、等腰梯形、正多边形、圆)的轴对称性及其相关性质.了解平行四边形、圆是中心对称图形.
④探索图形之间的变换关系(轴对称、平移、旋转及其组合).运用轴对称(或平移、旋转)及其组合进行图案设计;认识和欣赏轴对称(或平移、旋转)在现实生活中的应用.
(2)图形的相似
考试内容:
比例的基本性质,线段的比,成比例线段,图形的相似及性质,三角形相似的条件,图形的位似,锐角三角函数,300,450,600角的三角函数值.
考试要求:
①了解比例的基本性质,了解线段的比、成比例线段,通过实例了解黄金分割.
②通过实例认识图形的相似,了解相似图形的性质.知道相似多边形的对应角相等,对应边成比例,面积的比等于对应边比的平方.
③了解两个三角形相似的概念,掌握两个三角形相似的条件.
④了解图形的位似,能够利用位似将一个图形放大或缩小.
⑤通过实例了解物体的相似,利用图形的相似解决一些实际问题(如利用相似测量旗杆的高度).
⑥通过实例认识锐角三角函数(sinA,cosA,tanA),知道300,450,600角的三角函数值;会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它对应的锐角.
⑦运用三角函数解决与直角三角形有关的简单实际问题.
3、图形与坐标
考试内容:
平面直角坐标系.
考试要求:
①认识并能画出平面直角坐标系;在给定的直角坐标系中,会根据坐标描出点的位置、由点的位置写出它的坐标.
②能在方格纸上建立适当的直角坐标系,描述物体的位置.
③在同一直角坐标系中,感受图形变换后点的坐标的变化.
④灵活运用不同的方式确定物体的位置.
4、图形与证明
(1)了解证明的含义
考试内容:
定义、命题、逆命题、定理,定理的证明,反证法.
考试要求:
①理解证明的必要性.
②通过具体的例子,了解定义、命题、定理的含义,会区分命题的条件(题设)和结论.
③结合具体例子,了解逆命题的概念,会识别两个互逆命题,并知道原命题成立其逆命题不一定成立.
④理解反例的作用,知道利用反例可以证明一个命题是错误的.
⑤通过实例,体会反证法的含义.
⑥掌握用综合法证明的格式,体会证明的过程要步步有据.
(2)掌握证明的依据
考试内容:
一条直线截两条平行直线所得的同位角相等.
两条直线被第三条直线所截,若同位角相等,那么这两条直线平行.
若两个三角形的两边及其夹角分别相等,则这两个三角形全等.
两个三角形的两角及其夹边分别相等,则这两个三角形全等.
两个三角形的三边分别相等,则这两个三角形全等.
全等三角形的对应边、对应角分别相等.
考试要求:
运用以上6条“基本事实”作为证明的依据.
(3)利用(2)中的基本事实证明下列命题
考试内容:
①平行线的性质定理(内错角相等、同旁内角互补)和判定定理(内错角相等或同旁内角互补,则两直线平行).
②三角形的内角和定理及推论(三角形的外角等于不相邻的两内角的和,三角形的外角大于任何一个和它不相邻的内角).
③直角三角形全等的判定定理.
④角平分线性质定理及逆定理;三角形的三条角平分线交于一点(内心).
⑤垂直平分线性质定理及逆定理;三角形的三边的垂直平分线交干一点(外心).
⑥三角形中位线定理.
⑦等腰三角形、等边三角形、直角三角形的性质和判定定理.
⑧平行四边形、矩形、菱形、正方形、等腰梯形的性质和判定定理.
考试要求:
①会利用(2)中的基本事实证明上述命题.
②会利用上述定理证明新的命题.
③练习和考试中与证明有关的题目难度,应与上述所列的命题的论证难度相当.
(4)通过对欧几里得《原本》的介绍,感受几何的演绎体系对数学发展和人类文明的价值.
(三)统计与概率
1、统计
考试内容:
数据,数据的收集、整理、描述和分析.
抽样,总体,个体,样本.
扇形统计图.
加权平均数,数据的集中程度与离散程度,极差和方差.
频数、频率,频数分布,频数分布表、直方图、折线图.
样本估计总体,样本的平均数、中位数、众数、方差,总体的平均数、方差.
统计与决策,数据信息,统计在社会生活及科学领域中的应用.
考试要求:
①会收集、整理、描述和分析数据,能用计算器处理较为复杂的统计数据.
②了解抽样的必要性,能指出总体、个体、样本.知道不同的抽样可能得到不同的结果.
③会用扇形统计图表示数据.
④理解并会计算平均数、加权平均数、中位数、众数,能根据具体问题,选择合适的统计量表示数据的不同特征与集中程度.
⑤会探索如何表示一组数据的离散程度,会计算极差与方差,并会用它们表示数据的离散程度.
⑥理解频数、频率的概念,了解频数分布的意义和作用.会列频数分布表,画频数分布直方图和频数折线图,并能解决简单的实际问题.
⑦体会用样本估计总体的思想,能用样本的平均数、方差来估计总体的平均数和方差.
⑧能根据统计结果做出合理的判断和预测,体会统计对决策的作用,能比较清晰的表达自己的观点,并进行交流.
⑨能根据问题查找相关资料,获得数据信息,会对日常生活中的某些数据发表自己的看法.
⑩能应用统计知识解决在社会生活及科学领域中一些简单的实际问题.
2、概率
考试内容:
事件、事件的概率,列举法(包括列表、画树状图)计算简单事件的概率.
实验与事件发生的频率,大量重复实验时事件发生概率的估计值.
运用概率知识解决实际问题.
考试要求:
①在具体情境中了解概率的意义,运用列举法(包括列表、画树状图)计算简单事件发生的概率.
②通过实验,获得事件发生的频率;知道大量重复实验时频率可作为事件发生概率的估计值.
③能运用概率知识解决一些实际问题.
(四)课题学习
考试内容:
课题的提出,数学模型,问题解决.
数学知识的应用,研究问题的方法.
考试要求:
①经历“问题情境——建立模型——求解——解释与应用”的基本过程.
②体验数学知识之间的内在联系,初步形成对数学整体性的认识.
③获得一些研究问题的方法和经验,发展思维能力,加深理解相关的数学知识.
六、考试形式
初中毕业生数学学业考试采用闭卷笔试形式,全卷满分150分,考试时间120分钟.考试时必须携带计算器进入考场.
七、试卷难度
试题按其难度分为容易题、中档题和稍难题.难度值在0.70以上的试题为容易题,难度值在<, SPAN lang=EN-US>0.50—0.70之间的试题为中档题,难度值在0.30—0.50之间的试题为稍难题.三种试题(容易题、中档题和稍难题)分值之比约为8∶1∶1.
八、试卷结构
试题分选择题、填空题和解答题三种题型,选择题是四选一型的单项选择题;填空题只要求直接填写结果,不必写出计算过程或推证过程;解答题包括计算题、证明题、应用题、作图题等,解答题应写出文字说明、演算步骤、推证过程或按题目要求正确作图.三种题型的占分比例约为:选择题占16%,填空题占24%,解答题占60%(其中选择题约有6小题,填空题约有12小题,解答题约有10小题),全卷总题量约为28题. 同时,试卷还面向学习困难生设置难度较低的附加题(共10分),如果考生全卷得分低于90分(及格线),则附加题得分将计入全卷总分,但计入后全卷总分最多不超过90分;如果考生全卷得分已经达到或超过90分,则附加题得分不计入全卷总分.
九、试题示例
(一)选择题(A、B、C、D四个答案中只有一个正确,请你把正确答案前的字母填在括号内)
1、下列运算正确的是( ).
A、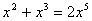 ; B、 ; B、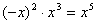 ; ;
C、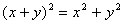 ; D、 ; D、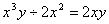 (容易题) (容易题)
2、世界文化遗产长城总长约6700000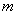 ,用科学记数法可表示为( ). ,用科学记数法可表示为( ).
A、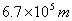 ; B、 ; B、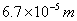 ; C、 ; C、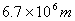 ; D、 ; D、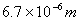 (容易题) (容易题)
3、数学教师对小王在参加中考前的5次数学模拟考试进行统计分析,若要判断小王的数学成绩是否稳定,该数学教师应该知道小王这5次数学成绩的( ).
 A、方差或极差;B、平均数或中位数;C、众数或频率; D、频数或众数(容易题) A、方差或极差;B、平均数或中位数;C、众数或频率; D、频数或众数(容易题)
 4、如右图,在 ABCD中,E、G是AD的三等分点, 4、如右图,在 ABCD中,E、G是AD的三等分点,
F、H是BC的三等分点,则图中平行四边形共有( ).
 A、3个; B、4个; C、5个; D、6个(容易题) A、3个; B、4个; C、5个; D、6个(容易题)
5、如右图,在Rt△ABC中,∠C=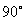 ,AC=2,BC的长为常数,点P从起点C出发,沿CB向终点B运动,设点P所走过路程CP的长为x,△APB的面积为y,则下列图象能大致反映y与x之间的函数关系的是( ). ,AC=2,BC的长为常数,点P从起点C出发,沿CB向终点B运动,设点P所走过路程CP的长为x,△APB的面积为y,则下列图象能大致反映y与x之间的函数关系的是( ).
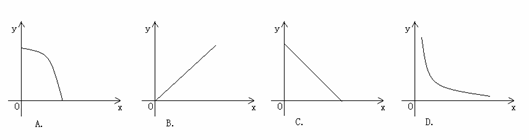
(中档题)
(二)填空题
6、 与 与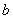 互为相反数,则 互为相反数,则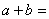 .(容易题) .(容易题)
7、代数式 可表示的实际意义是(写出一个例子即可) 可表示的实际意义是(写出一个例子即可)
.(容易题)
8、 某商品每件进价200元,现加价10%出售,则每件商品可获利润 ______元.(容易题)
9.因式分解: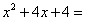 __________.(容易题) __________.(容易题)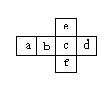
10、如图是一个正方体的平面展开图,每个面内都标注了字母,则面a 在展开前所对的面是 (填字母). (容易题)
 11、一个口袋有4个白球、1个红球、7个黄球,搅匀后随机地从中摸出一个球,摸到白球的概率是 .(容易题) 11、一个口袋有4个白球、1个红球、7个黄球,搅匀后随机地从中摸出一个球,摸到白球的概率是 .(容易题)
12、如图,⊙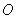 为 为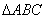 的外接圆, 的外接圆,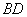 为直 为直
径,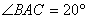 ,若 ,若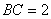 ,则 ,则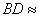
(精确到0.01).(中档题)
13、如果圆锥的底面周长是20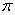 ,侧面展开图所得 ,侧面展开图所得
的扇形的圆心角为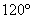 ,那么该圆锥的全面积为 .(中档题) ,那么该圆锥的全面积为 .(中档题)
14、四边形ABCD为边长等于1的菱形,顺次连结它的各边中点组成四边形EFGH(四边形EFGH称为原四边形ABCD的中点四边形),再顺次连结四边形EFGH的各边中点组成第二个中点四边形,……,则按上述规律组成的第八个中点四边形的边长等于 .(中档题)
(三)解答题
15、计算: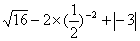 (容易题) (容易题)
16、先化简,再求值: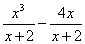 ,其中 ,其中 (容易题) (容易题)
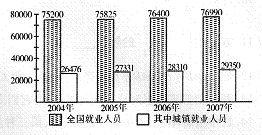
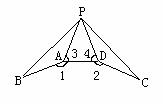
17、右图为2004-2007年全国就业和城镇就业人数(单位:万人)统计图.
根据图中信息,解答下列问题:
(1)2007年比2004年全国就业人员增加多少万人?
(2)哪一年全国非城镇就业人员最多? 该年全国非城填就业人员为多少万人? (容易题)
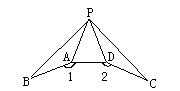
18、如图,已知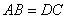 , ,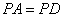 , ,
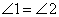 ,求证: ,求证: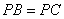 .(容易题) .(容易题)
19、在左图的方格纸中有一个Rt△ABC(A、B、C三点均为格点),∠C=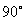 . .
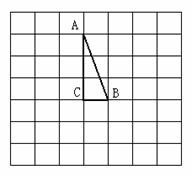 (1)请你画出将Rt△ABC绕点C顺时针旋转 (1)请你画出将Rt△ABC绕点C顺时针旋转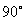 后所得到的Rt△ 后所得到的Rt△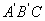 ,其中A、B的对应点分别是 ,其中A、B的对应点分别是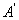 、 、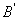 (不必写画法); (不必写画法);
(2)设(1)中AB的延长线与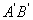 相交于D点,方格纸中每一个小正方形的边长为1,试求BD的长(精确到0.1).(中档题) 相交于D点,方格纸中每一个小正方形的边长为1,试求BD的长(精确到0.1).(中档题)
20、已知正n边形的周长为60,边长为a.
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的
边长为b.有人分别取n等于3、20、120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.(中档题)
21、李明从泉州乘汽车沿高速公路前往A地,已知该汽车的平均速度是100
千米/时,它行驶t小时后距泉州的路程为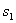 千米. 千米.
(1)请用含t的代数式表示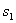 ; ;
(2)设另有王红同时从A地乘汽车沿同一条高速公路回泉州,已知这辆汽车距泉
州的路程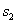 (千米)与行驶时间t(时)之间的函数关系式为 (千米)与行驶时间t(时)之间的函数关系式为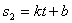 ( (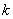 、 、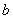 为常数, 为常数,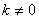 ),若王红从A地回到泉州用了9小时,且当 ),若王红从A地回到泉州用了9小时,且当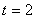 时, 时,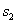 =560. =560.
①求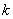 与 与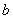 的值; 的值;
②试问在两辆汽车相遇之前,当行驶时间t的取值在什么范围内,两车的距离小于288千米?(稍难题)
22、已知:抛物线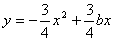 经过点 经过点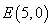 . .
(1)求b的值;
(2)设一正方形ABCD的顶点A、B在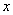 轴上(点A在点B的左侧),顶点C、 轴上(点A在点B的左侧),顶点C、
D在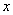 轴上方的抛物线上,O为坐标原点. 轴上方的抛物线上,O为坐标原点.
①求此正方形的边长;
②在∠COB的内部是否存在着点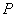 ,使得⊙ ,使得⊙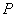 与 与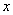 轴、直线BC、直线OC都 轴、直线BC、直线OC都
相切?若存在,请求出点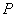 的坐标;若不存在,请说明理由.(稍难题) 的坐标;若不存在,请说明理由.(稍难题)
〔试题示例的参考答案或解答提示〕
(一)选择题:1、B; 2、C;3、A;4、D;5、C.
(二)填空题:6、0;7、略;8、20;9.(x+2)2;10、C;11、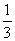 ;12、5.85; ;12、5.85;
13、400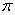 ;14、 ;14、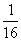 . .
(三)解答题:
15、解:原式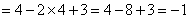
16、解:原式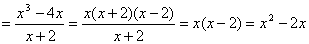
当 时,原式 时,原式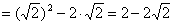
17、解:(1)1790万人;(2)2004年,48724万人.
18、证明:如右图,∵ 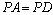 ,∴ ,∴ , ,
又∵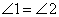 ; ;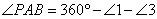 , ,
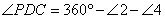 ,∴ ,∴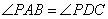 , ,
∵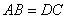 , ,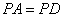 ,∴ ,∴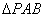 ≌ ≌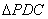 ,故得 ,故得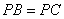 . .
19、略解:(1)图略;(2)先证明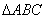 ∽ ∽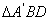 ,得 ,得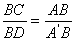 ,再求得 ,再求得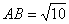 , ,
∴BD=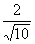 ≈0.6. ≈0.6.
20、解:(1)a=20 ; (2)此说法不正确,理由为:尽管当a = 3、20、120时,a >b或a<b, 但可令a = b, 得方程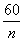 = = 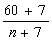 ,解得n = 60,经检验,n = 60是所得方程的根,∴当n= 60时,a = b,即不符合这一说法的n的值为60. ,解得n = 60,经检验,n = 60是所得方程的根,∴当n= 60时,a = b,即不符合这一说法的n的值为60.
21、解:(1)s1 = 100t;(2)①∵s2 = kt + b ,依题意得t = 9时,s2 = 0,又∵ t = 2时,s2 = 560 ∴ 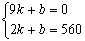 解得: 解得: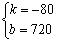
②由①得s2 = -80t + 720,令s1 = s2 ,得100t =-80t + 720, 解得t = 4.
当t<4时,s2>s1 ,∴s2-s1 <288,即(-80t + 720)-100t<288, -180t<
-432,∴180t>432,解得 t >2.4,∴在两车相遇之前,当2.4<t<4 时,两车的距离小于288千米.
22、解:(1)由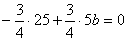 , 解得 , 解得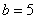 ;(2)①由(1) ;(2)①由(1)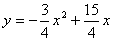 ,设 ,设 ,令 ,令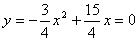 ,解得 ,解得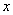 =0或 =0或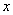 =5,由抛物线、正方形的性质 =5,由抛物线、正方形的性质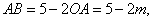 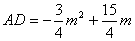 ,在正方形ABCD中,AD=AB,∴ ,在正方形ABCD中,AD=AB,∴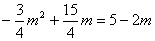 ,解得: ,解得: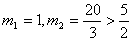 应舍去,∴取 应舍去,∴取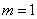 ,5-2 ,5-2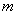 =3,∴正方形的边长为3 =3,∴正方形的边长为3
 ②点 ②点 存在.如图: 当点 存在.如图: 当点 在直线BC的左侧时,依题意知点 在直线BC的左侧时,依题意知点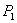 为△OBC的内心,作 为△OBC的内心,作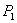 H⊥x轴于H,设△OBC的内切圆半径 H⊥x轴于H,设△OBC的内切圆半径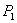 H为 H为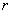 ,由①知:OB=4,BC=3,由勾股定理求得OC=5,∴ ,由①知:OB=4,BC=3,由勾股定理求得OC=5,∴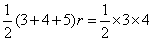 , 解得 , 解得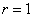 , ,
∵OH = OB-HB=4-1=3,则点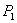 坐标为 坐标为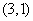 . .
当点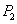 在直线BC的右侧时,作 在直线BC的右侧时,作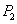 F⊥x轴于F, F⊥x轴于F,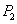 G⊥BC于G,设⊙ G⊥BC于G,设⊙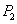 的半径为R,∵点 的半径为R,∵点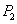 在 在 的平分线上,则 的平分线上,则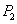 F= F=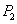 G=R, ∵ G=R, ∵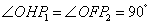 , ∴ , ∴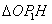 ∽ ∽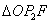 , ∴ , ∴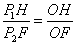 即 即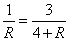 解得 解得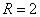
∵O F = OB+B F =4+2=6, 则点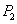 坐标为 坐标为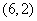
综上,点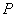 坐标为 坐标为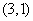 或 或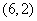 . .
|

